如图，已知△ABC内接于⊙O，AB是直径，点D在⊙O上，OD∥BC，过点D作DE⊥AB，垂足为E，连接CD交OE边于点F．（1）求证：△DOE∽△ABC；（2）求证：∠ODF=∠BDE；（3）连接OC，设△DOE的面积为S1，

Question

如图，已知△ABC内接于⊙O，AB是直径，点D在⊙O上，OD∥BC，过点D作DE⊥AB，垂足为E，连接CD交OE边于点F．

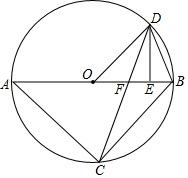
（1）求证：△DOE∽△ABC；
（2）求证：∠ODF=∠BDE；
（3）连接OC，设△DOE的面积为S₁，四边形BCOD的面积为S₂，若(S1)/(S2)=(2)/(7)，求sinA的值．

Answer 1

（1）证明：∵AB是⊙O的直径，
∴∠ACB=90°，
∵DE⊥AB，
∴∠DEO=90°，
∴∠DEO=∠ACB，
∵OD∥BC，
∴∠DOE=∠ABC，
∴△DOE～△ABC；

（2）证明：∵△DOE～△ABC，
∴∠ODE=∠A，
∵∠A和∠BDC是

BC

所对的圆周角，
∴∠A=∠BDC，
∴∠ODE=∠BDC，
∴∠ODF=∠BDE；

（3） ∵△DOE～△ABC，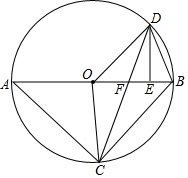
∴(S△DOE)/(S△ABC)=((OD)/(AB))2=(1)/(4)，
即S_△ABC=4S_△DOE=4S₁，
∵OA=OB，
∴S△BOC=(1)/(2)S△ABC，即S_△BOC=2S₁，
∵(S1)/(S2)=(2)/(7)，S2=S△BOC+S△DOE+S△DBE=2S1+S1+S△DBE，
∴S△DBE=(1)/(2)S1，
∴BE=(1)/(2)OE，
即OE=(2)/(3)OB=(2)/(3)OD，
∴sinA=sin∠ODE=(OE)/(OD)=(2)/(3)．