早教吧作业答案频道 -->物理-->
在直角坐标系中有P,Q两点,坐标如图所示,虚线是以原点为圆心的半圆,半圆与x轴围成的区域只存在垂直纸面向外的匀强磁场.大量的同种粒子从P点射入磁场,速度方向均在xy平面内,与
题目详情
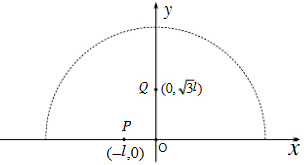
在直角坐标系中有P,Q两点,坐标如图所示,虚线是以原点为圆心的半圆,半圆与x轴围成的区域只存在垂直纸面向外的匀强磁场.大量的同种粒子从P点射入磁场,速度方向均在xy平面内,与轴正方向的夹角分布在0-180°范围内,粒子在磁场做圆周运动的半径R满足l≤R≤2l,所有粒子均不从半圆虚线边界射出.已知粒子质量为m(重力不计),带电量为q(q>0),磁感应强度大小为B.
求:(1)经过Q点时速度方向与y轴垂直的粒子的速度大小.
(2)求虚线半圆的最小半径和从P点运动到Q的粒子中运动时间的最大值和最小值.
求:(1)经过Q点时速度方向与y轴垂直的粒子的速度大小.
(2)求虚线半圆的最小半径和从P点运动到Q的粒子中运动时间的最大值和最小值.

▼优质解答
答案和解析
 (1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力有
(1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力有
qvB=m
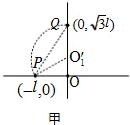
从甲图中可知:R=
解得v=
;
(2)当粒子以最大半径R=2l向x轴负方向发出打得粒子刚好与半圆相切时,虚线半圆的半径最小
由乙图的几何关系知:l2+R2=(r-R)2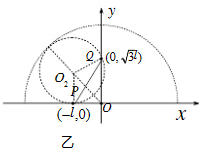
解得:虚线半圆的最小半径r=(2+
)l
带电粒子在磁场中运动的周期T=
从P点运动到Q点的粒子运动时间t1=
T(其中θ为PQ运动轨迹对应的圆心角)
从图丙中可知:以O3位圆心的粒子,圆心角最大,运动时间最长
由几何关系可知半径R=
l,且满足l<R<2l
由丙图可知圆心角θ=240°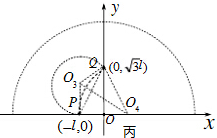
则从P点运动到Q的粒子运动时间最长为t1=
以Q4为圆心的粒子圆心角最小,运动时间最短
半径R=2l
由丙图知圆心角θ为60°
则从P点运动到Q的粒子运动时间最短为t2=
;
答:(1)经过Q点时速度方向与y轴垂直的粒子的速度大小为v=
;
(2)虚线半圆的最小半径为r=(2+
)l;从P点运动到Q的粒子中运动时间的最大值为t1=
,最小值为t2=
.
 (1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力有
(1)粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力有qvB=m
| v2 |
| R |
从甲图中可知:R=
| l |
| cos30° |
解得v=
2
| ||
| 3m |
(2)当粒子以最大半径R=2l向x轴负方向发出打得粒子刚好与半圆相切时,虚线半圆的半径最小
由乙图的几何关系知:l2+R2=(r-R)2

解得:虚线半圆的最小半径r=(2+
| 5 |
带电粒子在磁场中运动的周期T=
| 2πR |
| v |
从P点运动到Q点的粒子运动时间t1=
| θ |
| 360° |
从图丙中可知:以O3位圆心的粒子,圆心角最大,运动时间最长
由几何关系可知半径R=
2
| ||
| 3 |
由丙图可知圆心角θ=240°

则从P点运动到Q的粒子运动时间最长为t1=
| 4πm |
| 3qB |
以Q4为圆心的粒子圆心角最小,运动时间最短
半径R=2l
由丙图知圆心角θ为60°
则从P点运动到Q的粒子运动时间最短为t2=
| πm |
| 3qB |
答:(1)经过Q点时速度方向与y轴垂直的粒子的速度大小为v=
2
| ||
| 3m |
(2)虚线半圆的最小半径为r=(2+
| 5 |
| 4πm |
| 3qB |
| πm |
| 3qB |
看了 在直角坐标系中有P,Q两点,...的网友还看了以下:
如图所示,质量为m、电荷量为q的带电粒子,以初速度v0垂直射入场强为E方向竖直向下的匀强电场中,该 2020-05-13 …
如图所示的速度选择器水平放置,板长为L,两板间距离也为L,下板带正电,两板间电场强度大小为E,两板 2020-05-17 …
电子从静止出发被u的电压加速、沿着与电场垂直的方向进入另一个电场强度为e的匀强偏转电场、进入方向与 2020-06-06 …
两相邻匀强磁场区域的磁感应强度大小不同,方向平行.一速度方向与磁感应强度方向垂直的带电粒子(不计重 2020-06-25 …
两条平行虚线间存在一匀强磁场,磁感应强度方向与纸面垂直.边长为0.1m、总电阻为0.005Ω的正方 2020-07-01 …
如图所示,真空中一根绝缘杆连接的两个带等量异种电荷的点电荷以相同的角速度绕O点在水平面内匀速转动, 2020-07-08 …
图中a、b为两带正电的小球,带电量都是q,质量分别为M和m;用一绝缘弹簧联结,达到平衡时,弹簧的长 2020-07-09 …
如图,空间有一匀强磁场,一直金属棒与磁感应强度方向垂直,当它以速度v沿与棒和磁感应强度都垂直的方向 2020-07-29 …
拔河问题如果计绳重,在不平衡状态下(一方拉动绳子,绳子具有加速度)两方拉力不同拔河问题如果计绳重,在 2020-12-08 …
高中物理带电粒子在匀强磁场中的运动1.粒子速度越大半径越大圆心角越小所以在磁场中做匀速圆周运动时间越 2020-12-09 …