抛物线y=ax2+bx+c（a，b，c为常数，且a≠0）经过点（-1，0）和（m，0），且1<m<2，当x<-1时，y随着x的增大而减小．下列结论①a+b>0；②若点A（-3，y1），点B（-3，y2）都在抛物线上，则y1&

Question

抛物线y=ax²+bx+c（a，b，c为常数，且a≠0）经过点（-1，0）和（m，0），且1<m<2，当x<-1时，y随着x的增大而减小．下列结论①a+b>0；②若点A（-3，y₁），点B（-3，y₂）都在抛物线上，则y₁<y₂；③a（m-1）+b=0；④若c≤-1，则b²-4ac≤4a．其中正确结论的个数是（　　）

A. 1

B. 2

C. 3

D. 4

Answer 1

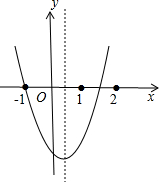∵抛物线过点（-1，0），当x<-1时，y随着x的增大而减小，
∴抛物线开口向上，
∴a>0，
∵抛物线经过点（-1，0）和（m，0），且1∴0<-(b)/(2a)<(1)/(2)，
∴a+b>0，所以①正确；
∵点A（-3，y₁），点B（3，y₂）都在抛物线上，
而点A到对称轴的距离比点B到对称轴的距离要大，
∴y₁>y₂，所以②错误；
∵抛物线经过点（-1，0）和（m，0），
∴a-b+c=0，am²+bm+c=0，
∴am²-a+bm-b=0，即a（m+1）（m-1）+b（m-1）=0，
∴a（m-1）+b=0，所以③正确；
∵c≤-1，
∴(4ac-b2)/(4a)<-1，
∴b²-4ac>4a，所以④错误．
故选B．