早教吧作业答案频道 -->数学-->
老师布置了这样一道作业题:在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB的度数.小聪提供了研究这个问题的过程和思路:先从特殊问
题目详情
老师布置了这样一道作业题:
在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB的度数.
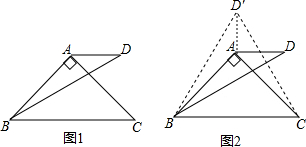
小聪提供了研究这个问题的过程和思路:先从特殊问题开始研究,当α=90°,β=30°时(如图1),利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形的相关知识便可解决这个问题.
(1)请结合小聪研究问题的过程和思路,求出这种特殊情况下∠ADB的度数;
(2)结合小聪研究特殊问题的启发,请解决老师布置的这道作业题.
在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB的度数.
小聪提供了研究这个问题的过程和思路:先从特殊问题开始研究,当α=90°,β=30°时(如图1),利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形的相关知识便可解决这个问题.
(1)请结合小聪研究问题的过程和思路,求出这种特殊情况下∠ADB的度数;
(2)结合小聪研究特殊问题的启发,请解决老师布置的这道作业题.

▼优质解答
答案和解析
(1)如图2中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′,
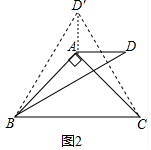
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,…(1分)
∵∠DBC=30°,
∴∠ABD=∠ABC-∠DBC=15°,
在△ABD和△ABD′中,
,
∴△ABD≌△ABD′,
∴∠ABD=∠ABD′=15°,∠ADB=∠AD′B,
∴∠D′BC=∠ABD′+∠ABC=60°,
∵BD=BD′,BD=BC,
∴BD′=BC,
∴△D′BC是等边三角形,
∴D′B=D′C,∠BD′C=60°,
在△AD′B和△AD′C中,
,
∴△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=
∠BD′C=30°,
∴∠ADB=30°.
(2) 第①种情况:当60°<α≤120°时,
如图3中,作∠AB D′=∠ABD,B D′=BD,连接CD′,AD′,
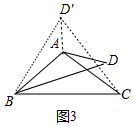
∵AB=AC,∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC=
=90°-
,
∴∠ABD=∠ABC-∠DBC=90°-
-β,
同(1)可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=90°-
-β,BD=BD′,∠ADB=∠AD′B
∴∠D′BC=∠ABD′+∠ABC=90°-
-β+90°-
=180°-(α+β),
∵α+β=120°,
∴∠D′BC=60°,
由(1)可知,△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=
∠BD′C=30°,
∴∠ADB=30°.
第②种情况:当0°<α<60°时,
如图4中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′.
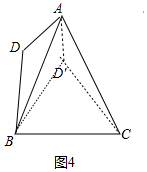
同理可得:∠ABC=
=90°-
,
∴∠ABD=∠DBC-∠ABC=β-(90°-
),
同(1)可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=β-(90°-
),BD=BD′,∠ADB=∠AD′B,
∴∠D′BC=∠ABC-∠ABD′=90°-
-[β-(90°-
)]=180°-(α+β),
∴D′B=D′C,∠BD′C=60°.
同(1)可证△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∵∠AD′B+∠AD′C+∠BD′C=360°,
∴∠ADB=∠AD′B=150°.

∵AB=AC,∠BAC=90°,
∴∠ABC=45°,…(1分)
∵∠DBC=30°,
∴∠ABD=∠ABC-∠DBC=15°,
在△ABD和△ABD′中,
|
∴△ABD≌△ABD′,
∴∠ABD=∠ABD′=15°,∠ADB=∠AD′B,
∴∠D′BC=∠ABD′+∠ABC=60°,
∵BD=BD′,BD=BC,
∴BD′=BC,
∴△D′BC是等边三角形,
∴D′B=D′C,∠BD′C=60°,
在△AD′B和△AD′C中,
|
∴△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=
| 1 |
| 2 |
∴∠ADB=30°.
(2) 第①种情况:当60°<α≤120°时,
如图3中,作∠AB D′=∠ABD,B D′=BD,连接CD′,AD′,

∵AB=AC,∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC=
| 180-α |
| 2 |
| α |
| 2 |
∴∠ABD=∠ABC-∠DBC=90°-
| α |
| 2 |
同(1)可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=90°-
| α |
| 2 |
∴∠D′BC=∠ABD′+∠ABC=90°-
| α |
| 2 |
| α |
| 2 |
∵α+β=120°,
∴∠D′BC=60°,
由(1)可知,△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=
| 1 |
| 2 |
∴∠ADB=30°.
第②种情况:当0°<α<60°时,
如图4中,作∠ABD′=∠ABD,BD′=BD,连接CD′,AD′.

同理可得:∠ABC=
| 180°-α |
| 2 |
| α |
| 2 |
∴∠ABD=∠DBC-∠ABC=β-(90°-
| α |
| 2 |
同(1)可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=β-(90°-
| α |
| 2 |
∴∠D′BC=∠ABC-∠ABD′=90°-
| α |
| 2 |
| α |
| 2 |
∴D′B=D′C,∠BD′C=60°.
同(1)可证△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∵∠AD′B+∠AD′C+∠BD′C=360°,
∴∠ADB=∠AD′B=150°.
看了 老师布置了这样一道作业题:在...的网友还看了以下:
在三角形ABC中,角BAC=90度,AB=AC,AE是过点A的一条直线,BD垂直AE于D,CF垂直 2020-04-07 …
2道超级无敌简单的数学题1.若|A|=|B|,杂下列叙述正确的是()A.A=BB.A=-BC.-A 2020-05-20 …
如图1所示,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在A 2020-06-20 …
1.直三棱柱ABC--A'B'C'中,各侧棱和底面的边长均为a,点D是侧棱CC'上任意一点,连接A 2020-06-27 …
(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同 2020-07-13 …
如图1所示,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在AE的异侧 2020-07-22 …
如图1,A是在数轴上一定点,A表示的数是5,B是数轴上一动点,B从原点O出发沿数轴正方向运动,速度 2020-07-30 …
高二数学在直三棱柱(侧棱垂直于底面的三棱柱)ABO-A1B1O1中OO1=4OA=4OB=3角AO 2020-07-30 …
在长方体ABCD-A'B'C'D',底面是边长为2的正方形,高为4,则点A'到截面AB'D'的距离 2020-08-02 …
(2013•房山区二模)已知:如图,点C、D在线段AB上,E、F在AB同侧,DE与CF相交于点O,且 2020-12-10 …