早教吧作业答案频道 -->数学-->
已知函数f(x)=exx-kx(e为自然对数的底数)有且只有一个零点,则实数k的取值范围是()A.(0,2)B.(0,e24)C.(0,e)D.(0,+∞)
题目详情
已知函数f(x)=
-kx(e为自然对数的底数)有且只有一个零点,则实数k的取值范围是( )ex x
A. (0,2)
B. (0,
)e2 4
C. (0,e)
D. (0,+∞)
▼优质解答
答案和解析
 f(x)=0,即
f(x)=0,即
-kx=0,
∵x≠0,
∴k=
,
令g(x)=
,
则g′(x)=
,
令g′(x)=0,解得x=1,
当x>2或x<0时,g′(x)>0,函数g(x)单调递增,
当0<x<2时,g′(x)<0,函数g(x)单调递增,
∴当x=2时,函数有极小值,即g(2)=
,
且当x<0,时,f(x)∈(0,+∞),
∵函数f(x)=
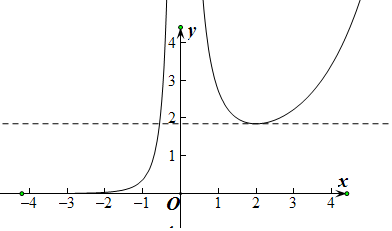
-kx(e为自然对数的底数)有且只有一个零点,结合图象可得,
∴0<k<
,
故选:B
 f(x)=0,即
f(x)=0,即| ex |
| x |
∵x≠0,
∴k=
| ex |
| x2 |
令g(x)=
| ex |
| x2 |
则g′(x)=
| ex(x-2) |
| x3 |
令g′(x)=0,解得x=1,
当x>2或x<0时,g′(x)>0,函数g(x)单调递增,
当0<x<2时,g′(x)<0,函数g(x)单调递增,
∴当x=2时,函数有极小值,即g(2)=
| e2 |
| 4 |
且当x<0,时,f(x)∈(0,+∞),
∵函数f(x)=
| ex |
| x |
∴0<k<
| e2 |
| 4 |
故选:B
看了 已知函数f(x)=exx-k...的网友还看了以下:
f(x)=x^2-2kx+k+1在[k,+∞)上为闭函数,求k取值范围x^2-2kx+k+1=xx 2020-06-11 …
已知f(x)=|x-k|+|x-2k|(k>0).(1)当x属于R,k为常数时,求f(x)的最小值 2020-06-11 …
如果x~b(15,1\4),则使P(X=k)取最大值的k值为A.3B.4C.5D.3或4 2020-06-12 …
已知函数f(x)=3x2+2(k-1)x+k+5(k∈R)(1)对任意k∈(-1,1),不等式f( 2020-06-12 …
如果m、n是定值,关于y的一元一次方程2ky+m/3-y-nk/6=2,对于k取任何值,方程的解总 2020-06-12 …
对于k取互为相反数的两个反比例函数来说,他们是关于x轴和y轴() 2020-06-15 …
若lnx/(x-1)+1/x大于lnx/(x+1)+k/x对于x大于o且不等于1恒成立,求k取值范围 2020-11-10 …
设f(x)=x/(e^-2+x^2),g(x)=(e^x)/x对任意x1若有恒成立,则正数k的取值范 2020-12-22 …
设f(x)=x/(e^-2+x^2),g(x)=(e^x)/x对任意x1若有恒成立,则正数k的取值范 2020-12-22 …
已知总体X是离散型随机变量X的可能取值为0,1,2且P{X=2}=(1-θ)^2E(X)=2(1-θ 2020-12-31 …