早教吧作业答案频道 -->数学-->
已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;(2)若点P在线段AB上.①如图2,连
题目详情
已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
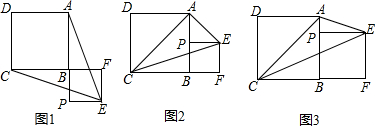
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.

(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
▼优质解答
答案和解析
(1)∵四边形ABCD和四边形BPEF是正方形,
∴AB=BC,BP=BF,
∴AP=CF,
在△APE和△CFE中,
,
∴△APE≌△CFE,
∴EA=EC;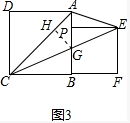
(2)①∵P为AB的中点,
∴PA=PB,又PB=PE,
∴PA=PE,
∴∠PAE=45°,又∠DAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
②∵EP平分∠AEC,EP⊥AG,
∴AP=PG=a-b,BG=a-(2a-2b)=2b-a
∵PE∥CF,
∴
=
,即
=
,
解得,a=
b;
作GH⊥AC于H,
∵∠CAB=45°,
∴HG=
AG=
×(2
b-2b)=(2-
)b,又BG=2b-a=(2-
)b,
∴GH=GB,GH⊥AC,GB⊥BC,
∴∠HCG=∠BCG,
∵PE∥CF,
∴∠PEG=∠BCG,
∴∠AEC=∠ACB=45°.
∴a:b=
:1;∴∠AEC=45°.
∴AB=BC,BP=BF,
∴AP=CF,
在△APE和△CFE中,
|
∴△APE≌△CFE,
∴EA=EC;

(2)①∵P为AB的中点,
∴PA=PB,又PB=PE,
∴PA=PE,
∴∠PAE=45°,又∠DAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
②∵EP平分∠AEC,EP⊥AG,
∴AP=PG=a-b,BG=a-(2a-2b)=2b-a
∵PE∥CF,
∴
| PE |
| BC |
| PG |
| GB |
| b |
| a |
| a-b |
| 2b-a |
解得,a=
| 2 |
作GH⊥AC于H,
∵∠CAB=45°,
∴HG=
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| 2 |
∴GH=GB,GH⊥AC,GB⊥BC,
∴∠HCG=∠BCG,
∵PE∥CF,
∴∠PEG=∠BCG,
∴∠AEC=∠ACB=45°.
∴a:b=
| 2 |
看了 已知正方形ABCD,P为射线...的网友还看了以下:
如图所示,在一个原来不带电的金属导体壳的球心处放一正电荷,则A、B、C三点的场强为()A.EA≠0 2020-05-16 …
如图所示,AB是一个固定在竖直面内的弧形轨道,与竖直圆形轨道BCD在最低点B平滑连接,且B点的切线 2020-06-17 …
已知:如图,在菱形ABCD中,分别延长AB、AD到E、F,使得BE=DF,连接EC、FC.求证:E 2020-07-15 …
已知:如图,在菱形ABCD中,分别延长AB、AD到E、F,使得BE=DF,连接EC、FC.求证:E 2020-07-15 …
下列各句中,加点的词语使用恰当的一项是()A.今年是奥运年,各种赛事鳞次栉比,令人目不暇接.B.知 2020-07-15 …
如图,在O中,E是弧AB的中点,C为O上的一动点(C与E在AB异侧),连接EC交AB于点F,EB= 2020-07-29 …
(2014•白银)如图,边长为1的正方形ABCD中,点E在CB延长线上,连接ED交AB于点F,AF 2020-08-01 …
如图,E、F分别为直角三角形ABC的直角边AC和斜边AB的中点,沿EF将△AEF折起到△A′EF的位 2020-11-02 …
下列句中划线的成语,运用恰当的一项是()A.庐山风景区景点很多,可以说风景络绎不绝,令我们目不暇接. 2020-11-15 …
如图所示是游乐场中过山车的实物图片,左图所示是过山车的简化模型图.在模型图中水平倾角都为α=37°, 2020-11-25 …