早教吧作业答案频道 -->数学-->
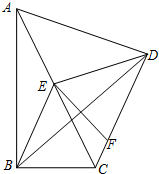
如图,已知在△ABC中,∠ABC=90°,点E是AC的中点,联结BE,过点C作CD∥BE,且∠ADC=90°,在DC取点F,使DF=BE,分别联结BD、EF.(1)求证:DE=BE;(2)求证:EF垂直平分BD.
题目详情
如图,已知在△ABC中,∠ABC=90°,点E是AC的中点,联结BE,过点C作CD∥BE,且∠ADC=90°,在DC取点F,使DF=BE,分别联结BD、EF.
(1)求证:DE=BE;
(2)求证:EF垂直平分BD.

(1)求证:DE=BE;
(2)求证:EF垂直平分BD.
▼优质解答
答案和解析
(1)证明:∵∠ABC=90°,∠ADC=90°,点E是AC的中点,
∴BE=
AC,DE=
AC.(直角三角形斜边上的中线等于斜边的一半)
∴BE=DE.
(2)证明:∵CD∥BE,
∴∠BEF=∠DFE.
∵DF=BE,BE=DE,
∴DE=DF.
∴∠DEF=∠DFE.
∴∠BEF=∠DEF.
∴EF垂直平分BD.(等腰三角形三线合一)
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=DE.
(2)证明:∵CD∥BE,
∴∠BEF=∠DFE.
∵DF=BE,BE=DE,
∴DE=DF.
∴∠DEF=∠DFE.
∴∠BEF=∠DEF.
∴EF垂直平分BD.(等腰三角形三线合一)
看了 如图,已知在△ABC中,∠A...的网友还看了以下:
在正方体ABCDA1B1C1D1中,M E F N 是A1B1 B1C1 C1D1 D1A1的中点 2020-05-13 …
2道几何题已知:P是正方形ABCD对角线BD上一点.PE垂直DC.PF垂直BC.E.F分别为垂足. 2020-05-13 …
如图①,四边形ABCD是平行四边形,对角线AC,BD相交于点O,过点O做直线EF分别交AD,BC于 2020-05-15 …
如图,在正方体ABCD-A1B1C1D1中,点F.F分别是棱AA1,CC1的中点,求证D1,E,F 2020-05-16 …
如图,平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别相交于E,F,求证:四边形A如图 2020-05-16 …
一道三点共线的证明题目,难度较大四边形ABCD内接于圆,其边AB与DC的延长线交于点P,AD与BC 2020-06-27 …
如何求证C,D,E,F四点共圆.以知:圆1与圆2相交与点A,B,点P在BA的延长线上,割线PCD交 2020-07-31 …
一个导数问题的理解设f(x)在[a,b]上连续,在(a,b)内可导且不恒于常数,f(a)=f(b) 2020-07-31 …
如图所示,圆i是R他△ABC的内切圆,角C=90°,圆i和三边分别相切于点D,E,F.如图,圆I是 2020-08-01 …
1.在平行边形ABCD中,AC,BD相交于点O,AE⊥BC于E,EO的延长线交AD于F,求证:四边形 2020-11-10 …