早教吧作业答案频道 -->数学-->
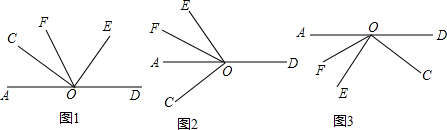
O为直线AD上一点,以O为顶点作∠COE=90°,射线OF平分∠AOE.(1)如图1,∠AOC与∠DOE的数量关系为,∠COF和∠DOE的数量关系为;(2)若将∠COE绕点O旋转至图2的位置,OF仍然平分∠AOE,
题目详情
O为直线AD上一点,以O为顶点作∠COE=90°,射线OF平分∠AOE.
(1)如图1,∠AOC与∠DOE的数量关系为___,∠COF和∠DOE的数量关系为___;
(2)若将∠COE绕点O旋转至图2的位置,OF仍然平分∠AOE,请写出∠COF和∠DOE之间的数量关系,并说明理由;
(3)若将∠COE绕点O旋转至图3的位置,射线OF仍然平分∠AOE,请写出∠COF和∠DOE之间的数量关系,并说明理由.
(1)如图1,∠AOC与∠DOE的数量关系为___,∠COF和∠DOE的数量关系为___;
(2)若将∠COE绕点O旋转至图2的位置,OF仍然平分∠AOE,请写出∠COF和∠DOE之间的数量关系,并说明理由;
(3)若将∠COE绕点O旋转至图3的位置,射线OF仍然平分∠AOE,请写出∠COF和∠DOE之间的数量关系,并说明理由.

▼优质解答
答案和解析
(1)∵∠COE=90°,∠COE+∠AOC+∠DOE=180°,
∴∠AOC+∠DOE=90°,
∵射线OF平分∠AOE,
∴∠AOF=∠EOF=
∠AOE,
∴∠COF=∠AOF-∠AOC=
∠AOE-(90°-∠DOE)=
(180°-∠DOE)-90°+∠DOE=
∠DOE,
故答案为:互余,∠COF=
∠DOE;
(2)∠COF=
∠DOE
∵OF平分∠AOE,
∴∠AOF=
∠AOE,
∵∠COE=90°,
∴∠AOC=90°-∠AOE,
∴∠COF=∠AOC+∠AOF=90°-∠AOE+
∠AOE=90°-
∠AOE,
∵∠AOE=180°-∠DOE,
∴∠COF=90°-
(180°-∠DOE)=
∠DOE,
即∠COF=
∠DOE;
(3)∠COF=180°-
∠DOE.
∵OF平分∠AOE,
∴∠EOF=
∠AOE,
∴∠COF=∠COE+∠EOF=90°+
∠AOE=90°+
(180°-∠DOE)=180°-
∠DOE,
即∠COF=180°-
∠DOE.
∴∠AOC+∠DOE=90°,
∵射线OF平分∠AOE,
∴∠AOF=∠EOF=
| 1 |
| 2 |
∴∠COF=∠AOF-∠AOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:互余,∠COF=
| 1 |
| 2 |
(2)∠COF=
| 1 |
| 2 |
∵OF平分∠AOE,
∴∠AOF=
| 1 |
| 2 |
∵∠COE=90°,
∴∠AOC=90°-∠AOE,
∴∠COF=∠AOC+∠AOF=90°-∠AOE+
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOE=180°-∠DOE,
∴∠COF=90°-
| 1 |
| 2 |
| 1 |
| 2 |
即∠COF=
| 1 |
| 2 |
(3)∠COF=180°-
| 1 |
| 2 |
∵OF平分∠AOE,
∴∠EOF=
| 1 |
| 2 |
∴∠COF=∠COE+∠EOF=90°+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠COF=180°-
| 1 |
| 2 |
看了 O为直线AD上一点,以O为顶...的网友还看了以下:
AB为圆O的直径点C为圆O上一点AD和过点C的切线互相垂直垂足为点D过点C作CE垂直AB垂足为点E直 2020-03-30 …
如图,AB是圆O的直径,BC为圆O的切线,AC交圆O与点E,D为AC上一点,且角AOD=角C 2020-03-30 …
(几何证明选讲选做题)PA与圆O切于A点,PCB为圆O的割线,且不过圆心O,已知∠BPA=30°, 2020-04-12 …
如图,PA与圆O相切点A,PCB为圆O的割线,并且不过圆心O,已知∠BPA=30°,PA=23,P 2020-04-12 …
如图,AC为圆O的直径,△ABD为圆O的内接三角形,AB=BD,BD交AC于F点,BE//AD交A 2020-04-27 …
如图,△ABC为圆O的内接三角形,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4 2020-05-13 …
已知,如图,AB为圆O的直径,圆O过AC的中点D,DE垂直BC于点E.《1》求证:DE为圆O的切线 2020-05-16 …
1.有一个圆O和两个正六边形T1,T2.T1的6个顶点都在圆周上.T2的6条边都和圆O相切(我们称 2020-05-20 …
一道九年级几何题,十万火急已知AB为圆o的直径,c为圆o上的一点,CD垂直AB于D,AD=9,BD 2020-06-05 …
(2013•潮州二模)如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=13DB,点C 2020-06-09 …