早教吧作业答案频道 -->数学-->
已知:Rt△ABC斜边AB上点D,E,满足∠DCE=45°.(1)如图1,当AC=1,BC=3,且点D与A重合时,求线段BE的长;(2)如图2,当△ABC是等腰直角三角形时,求证:AD2+BE2=DE2;(3)如图3,当AC=3,BC=4时
题目详情
已知:Rt△ABC斜边AB上点D,E,满足∠DCE=45°.
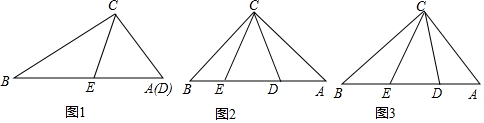
(1)如图1,当AC=1,BC=
,且点D与A重合时,求线段BE的长;
(2)如图2,当△ABC是等腰直角三角形时,求证:AD2+BE2=DE2;
(3)如图3,当AC=3,BC=4时,设AD=x,BE=y,求y关于x的函数关系式,并写出定义域.
(1)如图1,当AC=1,BC=
| 3 |
(2)如图2,当△ABC是等腰直角三角形时,求证:AD2+BE2=DE2;
(3)如图3,当AC=3,BC=4时,设AD=x,BE=y,求y关于x的函数关系式,并写出定义域.

▼优质解答
答案和解析
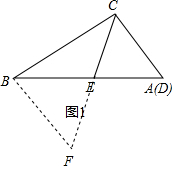 (1)如图1,∵∠ACB=90°,BC=
(1)如图1,∵∠ACB=90°,BC=
,AC=1,
∴AB=2,
过B作BF∥AC交CE的延长线于F,
∴∠F=∠ACE,
∵∠BCA=90°,∠DCE=45°,
∴∠BCE=∠DCE,
∴∠BCE=∠F,
∴BF=BC=
,
∵△BEF∽△AEC,
∴
=
=
,
∴BE=2-
;
(2)证明:过点A作AF⊥AB,使AF=BE,连接DF,CF,
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠B=45°,
∴∠FAC=45°,
∴△CAF≌△CBE(SAS),
∴CF=CE,
∠ACF=∠BCE,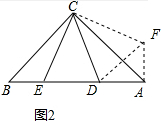
∵∠ACB=90°,∠DCE=45°,
∴∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,
∵∠ACF=∠BCE,
∴∠ACD+∠ACF=45°,
即∠DCF=45°,
∴∠DCF=∠DCE,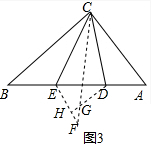
又∵CD=CD,
∴△CDF≌△CDE(SAS),
∴DF=DE,
∵AD2+AF2=DF2,
∴AD2+BE2=DE2;
(3)如图3,作△BCE≌△FCE,△GCD≌△ACD,延长DG交EF于H,
∵∠HFG=∠B,∠HGF=∠CGD=∠A,∠A+∠B=90°,
∴∠DHF=90°,
∵FG=1,∠B=∠F,
∴HF=
,HG=
,
∵EH2+HD2=ED2,
∴(y-
)2+(x+
)2=(5-x-y)2,
∴y=
(0≤x≤
).
 (1)如图1,∵∠ACB=90°,BC=
(1)如图1,∵∠ACB=90°,BC=| 3 |
∴AB=2,
过B作BF∥AC交CE的延长线于F,
∴∠F=∠ACE,
∵∠BCA=90°,∠DCE=45°,
∴∠BCE=∠DCE,
∴∠BCE=∠F,
∴BF=BC=
| 3 |
∵△BEF∽△AEC,
∴
| BE |
| AE |
| BF |
| AC |
| 3 |
∴BE=2-
| 3 |
(2)证明:过点A作AF⊥AB,使AF=BE,连接DF,CF,
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠B=45°,
∴∠FAC=45°,
∴△CAF≌△CBE(SAS),
∴CF=CE,
∠ACF=∠BCE,

∵∠ACB=90°,∠DCE=45°,
∴∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,
∵∠ACF=∠BCE,
∴∠ACD+∠ACF=45°,
即∠DCF=45°,
∴∠DCF=∠DCE,

又∵CD=CD,
∴△CDF≌△CDE(SAS),
∴DF=DE,
∵AD2+AF2=DF2,
∴AD2+BE2=DE2;
(3)如图3,作△BCE≌△FCE,△GCD≌△ACD,延长DG交EF于H,
∵∠HFG=∠B,∠HGF=∠CGD=∠A,∠A+∠B=90°,
∴∠DHF=90°,
∵FG=1,∠B=∠F,
∴HF=
| 4 |
| 5 |
| 3 |
| 5 |
∵EH2+HD2=ED2,
∴(y-
| 4 |
| 5 |
| 3 |
| 5 |
∴y=
| 60-28x |
| 21-5x |
| 15 |
| 7 |
看了 已知:Rt△ABC斜边AB上...的网友还看了以下:
若a.b为实数,且b= (a+1分之根号a²-1,+根号1-a²),+4,则a+b的值为?求具体的 2020-04-05 …
二次根式:1、√a^2b^5c^4(a<0)2、ab√1/a^4-1/b^4(b>a)在2点之前. 2020-05-14 …
关于"已知a>0,b>0 a+b=2则y=1/a+4/b的最小值"的困扰我知道将 a+b=2 代入 2020-05-15 …
已知函数f(x)=ax^3+bx^2-3x,a,b属于R.1.若f(x)是R上的单调函数,求a,b 2020-05-16 …
ab两数为正整数,怎么证明:a+b)(1/a+1/b)>4用均值不等式ab两数为正整数,怎么证明: 2020-06-03 …
在直线l:3x-y-5=0上找一点P,使P到A(5,1)B(4,4)的距离最小,求出最小值在直线l 2020-06-04 …
下面分四种情况讨论:(注:分类讨论是一种非常重要的数学思想方法)(1)当a=,b=时,a+b==; 2020-06-22 …
已知圆x^2+y^2+2x-4y+1=0关于直线2ax-by+2=0(a>0,b>0)对称,则4/ 2020-08-01 …
在网格内,三角形ABC三个顶点的坐标为A(-2,-1),B:(-4,-2),C(-3,-4),(1 2020-08-02 …
好的给QB(1)-12x的3次方y的4次方/(-3x的平方y的3次方)*(-1/3xy)(2)125 2020-10-30 …