早教吧作业答案频道 -->数学-->
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,PF=3FB.(1)证明:EF∥平面ABC;(2)若∠BAC=60°,求点P到平面BCD的距离.
题目详情
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,
=3
.
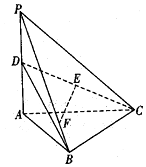
(1)证明:EF∥平面ABC;
(2)若∠BAC=60°,求点P到平面BCD的距离.
| PF |
| FB |

(1)证明:EF∥平面ABC;
(2)若∠BAC=60°,求点P到平面BCD的距离.
▼优质解答
答案和解析
(本小题满分12分)
(Ⅰ)证明:法一:如图,过点F作FM∥PA交AB于点M,
取AC的中点N,连接MN,EN.
∵点E为CD的中点,∴EN
AD.又PF=3FB,∴MF
AD,∴FM
EN,
所以四边形MFEN为平行四边形,
∴EF∥MN,∵EF⊄平面ABC,MN⊂平面ABC,
∴EF∥平面ABC.…(6分)
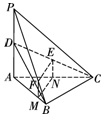
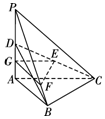
法二:如图,取AD中点G,连接GE,GF,则GE∥AC,GF∥AB,
因为GE∩GF=G,AC∩AB=A,所以平面GEF∥平面ABC,
所以EF∥平面ABC.…(6分)
(Ⅱ) ∵PA⊥平面ABC,∴PA⊥BC.
又BC⊥AB,AB∩PA=A,
∴BC⊥平面PAB.
又∠BAC=60°,AC=2,∴AB=1, BC=
, BD=
,
∴S△BCD=
BC • BD=
.
记点P到平面BCD的距离为d,则VP-BCD=VC-PBD,∴
S△BCD • d=
S△PBD • BC,
∴
• d=
PD • AB • BC⇒d=
,
所以,点P到平面BCD的距离为d=
. …(12分)
(Ⅰ)证明:法一:如图,过点F作FM∥PA交AB于点M,
取AC的中点N,连接MN,EN.
∵点E为CD的中点,∴EN
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
所以四边形MFEN为平行四边形,
∴EF∥MN,∵EF⊄平面ABC,MN⊂平面ABC,
∴EF∥平面ABC.…(6分)

法二:如图,取AD中点G,连接GE,GF,则GE∥AC,GF∥AB,
因为GE∩GF=G,AC∩AB=A,所以平面GEF∥平面ABC,
所以EF∥平面ABC.…(6分)

(Ⅱ) ∵PA⊥平面ABC,∴PA⊥BC.
又BC⊥AB,AB∩PA=A,
∴BC⊥平面PAB.
又∠BAC=60°,AC=2,∴AB=1, BC=
| 3 |
| 2 |
∴S△BCD=
| 1 |
| 2 |
| ||
| 2 |
记点P到平面BCD的距离为d,则VP-BCD=VC-PBD,∴
| 1 |
| 3 |
| 1 |
| 3 |
∴
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
所以,点P到平面BCD的距离为d=
| ||
| 2 |
看了 如图,三棱锥P-ABC中,P...的网友还看了以下:
读图,完成下列问题.(1)写出图中字母A、B的经纬度:A;B.A在B的方向.(2)C是海峡,是俄罗 2020-05-16 …
假定A为自变量,B为因变量,弹性的数学表达式为( )A.E=(△A/△B)·(B/A)B.E=(△B 2020-05-30 …
(2011•太原)如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠C 2020-06-12 …
设A=(101;020;-101)求满足方程AB+E=A^2+B的矩阵B用AB+E=A^2+B(A 2020-06-18 …
矩阵A=(101020101)且AB+E=A^2+B求B为何等式两边同乘A*就算出B=E呢?|A| 2020-06-20 …
有6个门铃按纽,但只有一个是真按纽.有一张告示:A在B的左边;B在C右边的第三个;C在D的右边;D 2020-06-21 …
逻辑题:ABCD在一起聊天,后来他们指责别人说假话:A:B说假话,B:不是C就是D说假话C:D和E 2020-07-19 …
设a,b为常数,X为随机变量,则下列关系正确的是()A,E(aX+b)=a^2E(X)+bB:E[ 2020-07-22 …
如图所示,A、B两点分别是斜面的顶端、底端,C、D是斜面上的两个点,LAC:LCD:LDB=1:3 2020-07-29 …
有关区间的定义问题让我们回忆实数集合R中区间的精确定义:R的子集E称为一个区间,如果它至少包含两个点 2020-11-20 …