早教吧作业答案频道 -->数学-->
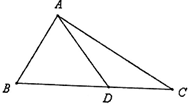
如图,D是直角△ABC斜边BC上一点,AC=3DC.(I)若∠DAC=30°,求角B的大小;(Ⅱ)若BD=2DC,且AD=22,求DC的长.
题目详情
如图,D是直角△ABC斜边BC上一点,AC=
DC.
(I)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD=2
,求DC的长.
| 3 |
(I)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD=2
| 2 |

▼优质解答
答案和解析
(本题满分为12分)
(Ⅰ)在△ABC中,根据正弦定理,有
=
.
因为AC=
DC,所以sin∠ADC=
sin∠DAC=
.
又∠ADC=∠B+∠BAD=∠B+60°>60°,
所以∠ADC=120°.…(3分)
于是∠C=180°-120°-30°=30°,所以∠B=60°.…(6分)
(Ⅱ)设DC=x,则BD=2x,BC=3x,AC=
x.
于是sinB=
=
,cosB=
,AB=
x.…(9分)
在△ABD中,由余弦定理,得 AD2=AB2+BD2-2AB•BDcosB,
即(2
)2=6x2+4x2-2×
x×2x×
=
(Ⅰ)在△ABC中,根据正弦定理,有
| AC |
| sin∠ADC |
| DC |
| sin∠DAC |
因为AC=
| 3 |
| 3 |
| ||
| 2 |
又∠ADC=∠B+∠BAD=∠B+60°>60°,
所以∠ADC=120°.…(3分)

于是∠C=180°-120°-30°=30°,所以∠B=60°.…(6分)
(Ⅱ)设DC=x,则BD=2x,BC=3x,AC=
| 3 |
于是sinB=
| AC |
| BC |
| ||
| 3 |
| ||
| 3 |
| 6 |
在△ABD中,由余弦定理,得 AD2=AB2+BD2-2AB•BDcosB,
即(2
| 2 |
| 6 |
| ||
| 3 |
作业帮用户
2017-03-23
看了 如图,D是直角△ABC斜边B...的网友还看了以下:
直角三角形问题1、在一个直角三角形ABC的内部作一个矩形BDEF,其中F和D分别在两直角边AB和A 2020-04-09 …
四边形cedf的面积会不会随三角尺的转动而发生变化在Rt△ABC中,∠C=90°,AC=BC=4, 2020-04-13 …
问一道初三几何题以直角三角形ABC的直角边AC为直径作圆,交斜边AB于点D,过点D作圆的切线.求证 2020-04-25 …
在三角形ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF平行AC交AC于点F,DE平行 2020-06-12 …
如图,在△ABC中,AB=AC,cosB=1/3,BC=2,点D,E,F分别在AC,AB,BC边上 2020-06-27 …
如图1,已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点.(1)求证:CD=BD;( 2020-07-09 …
如图,有一块直角三角形纸片,两直角边分别为AC=6cm,BC=8cm,现将ac沿直线AD折叠,使其 2020-07-15 …
在△ABC中,角c=90度,AC=6,BC=8,D和E分别是斜边AB和直角边CB上的点,把△ABC 2020-08-02 …
平面几何ΔABC中∠B=90°,∠A=30°,BC=6cm;ΔFDE中∠D=90°,∠E=45°, 2020-08-02 …
八年级数学题在△ABC中,BC=BA,角B=120度,AB垂直平分线交AC于D.求证:AD=(1/2 2021-02-01 …