早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.(1)求证:DE是⊙O的切线;(2)若CF=2,DF=4,求⊙O直径的长.
题目详情
如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
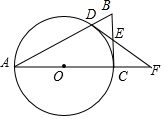
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.

(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.
▼优质解答
答案和解析
(1)如图,连接OD、CD,
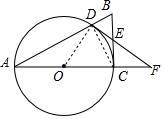
∵AC为⊙O的直径,
∴△BCD是直角三角形,
∵E为BC的中点,
∴BE=CE=DE,
∴∠CDE=∠DCE,
∵OD=OC,
∴∠ODC=∠OCD,
∵∠ACB=90°,
∴∠OCD+∠DCE=90°,
∴∠ODC+∠CDE=90°,即OD⊥DE,
∴DE是⊙O的切线;
(2)设⊙O的半径为r,
∵∠ODF=90°,
∴OD2+DF2=OF2,即r2+42=(r+2)2,
解得:r=3,
∴⊙O的直径为6.

∵AC为⊙O的直径,
∴△BCD是直角三角形,
∵E为BC的中点,
∴BE=CE=DE,
∴∠CDE=∠DCE,
∵OD=OC,
∴∠ODC=∠OCD,
∵∠ACB=90°,
∴∠OCD+∠DCE=90°,
∴∠ODC+∠CDE=90°,即OD⊥DE,
∴DE是⊙O的切线;
(2)设⊙O的半径为r,
∵∠ODF=90°,
∴OD2+DF2=OF2,即r2+42=(r+2)2,
解得:r=3,
∴⊙O的直径为6.
看了 如图,在Rt△ABC中,∠A...的网友还看了以下:
如图,△ABC中,点O在边AB上,过点O作BC的平行线交∠ABC的平分线于点D,过点B作BE⊥BD 2020-04-09 …
使用如图(a)所示的装置验证机械能守恒定律,打出一条纸带如图(b)所示.图(b)中O是打出的第一个 2020-06-19 …
如图,AC是O的直径,点B在O上,∠ACB=30°(1)利用尺规作∠ABC的平分线BD,交AC于点 2020-06-22 …
《新唐书》记载“(卢商)早孤,家贫困,能以学自奋。举进士,拔萃,皆中o"作为文献史料,此记载可用于 2020-07-02 …
如图,在正方形ABCD中,E是边CD的中点.(1)用直尺和圆规作O,使O经过点A、B、E(保留作图 2020-07-10 …
如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心,12AC长为半径作⊙O,交BC于E,过O 2020-07-21 …
如图,在RT△ABC中,∠ACB=90º,∠B=60º,BC=2,点O是AC中点如图,在RT△AB 2020-07-25 …
如图三角形oac中以o为圆心oa为半径作圆o作ob垂直oc交圆o于b,垂足为o连接ab交oc于d 2020-07-30 …
如图,已知在△ABC中,∠A,∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥A 2020-11-02 …
请用无刻度的直尺,根据下列条件分别找到图1中的圆心O和图2中的圆心P的位置.(保留作图痕迹,不写作法 2020-11-06 …