已知函数f（x）=ax+elnx与g（x）=x2x-elnx的图象有三个不同的公共点，其中e为自然对数的底数，则实数a的取值范围为（）A.a<-eB.a>1C.a>eD.a<-3或a>1

Question

已知函数f（x）=ax+elnx与g（x）=

(x2)/(x-elnx)的图象有三个不同的公共点，其中e为自然对数的底数，则实数a的取值范围为（　　）

A. a<-e

B. a>1

C. a>e

D. a<-3或a>1

Answer 1

由ax+elnx=(x2)/(x-elnx)，整理得：a+(elnx)/(x)=(1)/(1-(elnx)/(x))，
令h（x）=(elnx)/(x)，且t=h（x），
则t²+（a-1）t-a+1=0，
求导h′（x）=(e(1-lnx))/(x2)=0，解得：x=e，
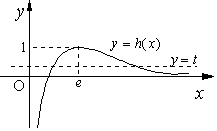
∴h（x）在（0，e）上单调递增，在（e，+∞）单调递减，
则当x→+∞时，h（x）→0，如图所示，
由题意可知方程有一个根t₁在（0，1）内，另一个根t₂=1或t₂=0或t₂∈（-∞，0），
当t₂=1方程无意义，当t₂=0时，a=1，t₁=0不满足题意；
则t₂∈（-∞，0），由二次函数的性质可知：

f(0)<0

f(1)>0

，即

-a+1<0

1+(a-1)-a+1>0

，
解得：a>1，
故选：B．