早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.(1)判断直线MN与O的位置关系,并说明理由;(2)若OA=4,∠BCM=60°,求图中阴
题目详情
如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
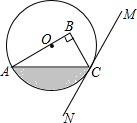
(1)判断直线MN与 O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.

(1)判断直线MN与 O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
▼优质解答
答案和解析
(1)MN是 O切线.
理由: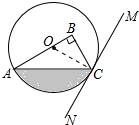 连接OC.
连接OC.
∵OA=OC,
∴∠OAC=∠OCA,
∵∠BOC=∠A+∠OCA=2∠A,∠BCM=2∠A,
∴∠BCM=∠BOC,
∵∠B=90°,
∴∠BOC+∠BCO=90°,
∴∠BCM+∠BCO=90°,
∴OC⊥MN,
∴MN是 O切线.
(2)由(1)可知∠BOC=∠BCM=60°,
∴∠AOC=120°,
在RT△BCO中,OC=OA=4,∠BCO=30°,
∴BO=
OC=2,BC=2
∴S阴=S扇形OAC-S△OAC=
-
•4•2
=
-4
.
理由:
 连接OC.
连接OC.∵OA=OC,
∴∠OAC=∠OCA,
∵∠BOC=∠A+∠OCA=2∠A,∠BCM=2∠A,
∴∠BCM=∠BOC,
∵∠B=90°,
∴∠BOC+∠BCO=90°,
∴∠BCM+∠BCO=90°,
∴OC⊥MN,
∴MN是 O切线.
(2)由(1)可知∠BOC=∠BCM=60°,
∴∠AOC=120°,
在RT△BCO中,OC=OA=4,∠BCO=30°,
∴BO=
| 1 |
| 2 |
| 3 |
∴S阴=S扇形OAC-S△OAC=
| 120π•42 |
| 360 |
| 1 |
| 2 |
| 3 |
| 16π |
| 3 |
| 3 |
看了 如图,在Rt△ABC中,∠B...的网友还看了以下:
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向 2020-06-11 …
如图,直线MN:y=-x+b与x轴交于点M(4,0),与y轴交于点N,长方形ABCD的边AB在x轴 2020-06-12 …
高中数学导学导练正方向上的单位向量问题已知两个恒力F1=i+2j,F2=4i-5j作用于同一质点, 2020-07-15 …
如图,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,由点A出发,沿边AB向 2020-07-24 …
在平角直角坐标系中,已知两点A(a—3,-5)和B(7,b+2)(1)若A、B关于y轴对称,求a与 2020-07-30 …
如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,点P、Q分别从A、C两点的位置同时 2020-11-04 …
一条信息可通过如图的网格线由上(点A)往下向各站点传送.例如信息到点b2可由经a1的站点到达(表示为 2020-11-28 …
如图所示,数轴上依次有三点A,O,B,点A位于原点O的左侧且相距40个单位长度,BO=30个单位长度 2020-12-19 …
已知两个力(单位:牛)f1与f2的夹角为60度.其中f1=(2,0),某质点在这两个力的共同作用下, 2020-12-21 …
平面直角坐标系中,一个动点从原点O出发向左平移2个单位长度,再向上平移4个单位长度到达点A,再由点A 2020-12-25 …