在平面直角坐标系xOy中，抛物线C：y=x2+（3-m）x经过点A（-1，0）．（1）求抛物线C的表达式；（2）将抛物线C沿直线y=1翻折，得到的新抛物线记为C1，求抛物线C1的顶点坐标；（3）将抛物线C沿

Question

在平面直角坐标系xOy中，抛物线C：y=x²+（3-m）x经过点A（-1，0）．
（1）求抛物线C的表达式；
（2）将抛物线C沿直线y=1翻折，得到的新抛物线记为C₁，求抛物线C₁的顶点坐标；
（3）将抛物线C沿直线y=n翻折，得到的图象记为C₂，设C与C₂围成的封闭图形为M，在图形M上内接一个面积为4的正方形（四个顶点均在M上），且这个正方形的边分别与坐标轴平行．求n的值．

Answer 1

（1）∵抛物线C：y=x²+（3-m）x经过点A（-1，0），
∴1-（3-m）=0．
∴m=2．
∴抛物线C的表达式为y=x²+x．

（2）∵抛物线C：y=x²+x=（x+(1)/(2)）²-(1)/(4)，
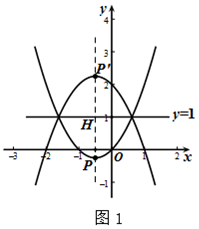
∴抛物线C的顶点为P(-(1)/(2)，-(1)/(4))，如图1，
点P(-(1)/(2)，-(1)/(4))关于直线y=1的对称点为P'(-(1)/(2)，(9)/(4))．
∴抛物线C₁的顶点坐标为(-(1)/(2)，(9)/(4))．

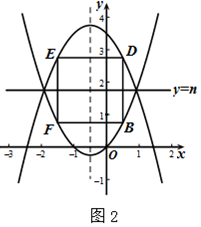（3）∵抛物线C：y=x²+x=（x+(1)/(2)）²-(1)/(4)，
∴抛物线的对称轴为x=-(1)/(2)，
∵正方形的边长为2，
∴正方形的顶点B的坐标为((1)/(2)，(3)/(4))，如图2．
∴n-(3)/(4)=1．
∴n=(7)/(4)．