早教吧作业答案频道 -->数学-->
如图,C为O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交O于D,∠PBH=2∠PAC.(1)求证:PC是O的切线;(2)若sin∠P=23,求BHBD的值.
题目详情
如图,C为 O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交 O于D,∠PBH=2∠PAC.
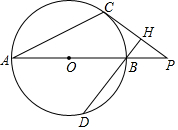
(1)求证:PC是 O的切线;
(2)若sin∠P=
,求
的值.

(1)求证:PC是 O的切线;
(2)若sin∠P=
| 2 |
| 3 |
| BH |
| BD |
▼优质解答
答案和解析
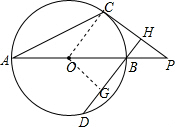 (1)证明:连接OC,
(1)证明:连接OC,
∵OA=OC,
∴∠PAC=∠OCA,
∴∠COP=∠PAC+∠OCA=2∠PAC,
∵∠PBH=2∠PAC,
∴∠COP=∠OBH,
∴OC∥BH,
∵BH⊥CP,
∴OC⊥CP,
∴PC是 O的切线;
(2) 设 O的半径为2a,
在Rt△OCP中,sin∠P=
,OC⊥CP,
∴OP=3a,
∴PB=OP-OB=a,
作OG⊥DH,
则BG=
BD,△OBG∽△PBH,
∴
=
=
,
∴
=
.
 (1)证明:连接OC,
(1)证明:连接OC,∵OA=OC,
∴∠PAC=∠OCA,
∴∠COP=∠PAC+∠OCA=2∠PAC,
∵∠PBH=2∠PAC,
∴∠COP=∠OBH,
∴OC∥BH,
∵BH⊥CP,
∴OC⊥CP,
∴PC是 O的切线;
(2) 设 O的半径为2a,
在Rt△OCP中,sin∠P=
| 2 |
| 3 |
∴OP=3a,
∴PB=OP-OB=a,
作OG⊥DH,
则BG=
| 1 |
| 2 |
∴
| BH |
| BG |
| BP |
| OB |
| 1 |
| 2 |
∴
| BH |
| BD |
| 1 |
| 4 |
看了 如图,C为O上的一点,P为直...的网友还看了以下:
在共点O三条不共面直线a,b,c上,在点O两侧分别取点A和A',B和B',C和C',且AO=A'O 2020-05-13 …
英语单词辨音找出画()部分读音与其余不同的单词()1.A .kn(ee) B.n(e)ck C.r 2020-05-17 …
已知O的半径为3,直线l到圆心O的距离为2,则直线l与O的位置关系是()A.相离B.相切C.相交D 2020-07-26 …
(2006•邵阳)已知⊙O的半径为3cm,点P是直线l上一点,OP长为5cm,则直线l与⊙O的位置 2020-07-26 …
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,且AB>AD+BC,AB是⊙O的直径,则直线 2020-07-26 …
⊙O的半径是6,点O到直线a的距离为5,则直线a与⊙O的位置关系为()A.相离B.相切C.相交D. 2020-07-26 …
已知O的半径是一元二次方程x2-6x+9=0的解,且点O到直线AB的距离为2,则O与直线AB的位置 2020-07-31 …
在直角坐标系中,圆O的圆心在原点,半径为3,圆A的圆心A的坐标为(负根3,1),半径为1,那么圆O 2020-07-31 …
在直角坐标系中,⊙O的圆心在原点,半径为3,⊙A的圆心A的坐标为,半径为1,那么⊙O与⊙A的位置关 2020-07-31 …
(2006•邵阳)已知⊙O的半径为3cm,点P是直线l上一点,OP长为5cm,则直线l与⊙O的位置关 2021-01-11 …