早教吧作业答案频道 -->数学-->
如图,在△ABC中,CD⊥AB,垂足为点D.以AB为直径的半⊙O分别与AC、CD相交于点E、F,连接AF、EF.(1)求证:∠AFE=∠ACD;(2)若CE=4,CB=45,tan∠CAB=43,求FD的长.
题目详情
如图,在△ABC中,CD⊥AB,垂足为点D.以AB为直径的半⊙O分别与
AC、CD相交于点E、F,连接AF、EF.
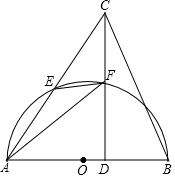
(1)求证:∠AFE=∠ACD;
(2)若CE=4,CB=4
,tan∠CAB=
,求FD的长.
AC、CD相交于点E、F,连接AF、EF.

(1)求证:∠AFE=∠ACD;
(2)若CE=4,CB=4
| 5 |
| 4 |
| 3 |
▼优质解答
答案和解析
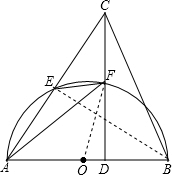 (1)证明:连接BE,
(1)证明:连接BE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠CAD+ABE=90°,
∵CD⊥AB,
∴∠CDA=90°,
∴∠CAD+∠ACD=90°,
∴∠ABE=∠ACD,
∵∠ABE=∠AFE,
∴∠AFE=∠ACD;
(2)连接OF,
∵∠BEC=90°,
∴BE=
=8,
∵tan∠CAB=
,
∴sin∠CAB=
,
∵AC=AE+CE=10,
∴CD=8,
∴AD=6,
∵OD=AD-OA=1,
∴OF=5,
∴DF=
=2
.
 (1)证明:连接BE,
(1)证明:连接BE,∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠CAD+ABE=90°,
∵CD⊥AB,
∴∠CDA=90°,
∴∠CAD+∠ACD=90°,
∴∠ABE=∠ACD,
∵∠ABE=∠AFE,
∴∠AFE=∠ACD;
(2)连接OF,
∵∠BEC=90°,
∴BE=
| CB2-CE2 |
∵tan∠CAB=
| 4 |
| 3 |
∴sin∠CAB=
| 4 |
| 5 |
∵AC=AE+CE=10,
∴CD=8,
∴AD=6,
∵OD=AD-OA=1,
∴OF=5,
∴DF=
| OF2-OD2 |
| 6 |
看了 如图,在△ABC中,CD⊥A...的网友还看了以下:
AB为圆O的直径点C为圆O上一点AD和过点C的切线互相垂直垂足为点D过点C作CE垂直AB垂足为点E直 2020-03-30 …
已知A,B,C,D四点共面且任三点不共线,面外空间一点P满足,向量AP=x向量PB+2向量PC-2 2020-05-13 …
AB为圆O的直径,点C为圆O上的一点,AD和过点C的切线互相垂直,垂足为点D过点D作CE垂直于AB 2020-05-21 …
如下,我知道是D求为什么在没有标出原点的数轴上A,B,C,D四点对应的有理数都是整数.且其中一个位 2020-06-06 …
(1/2)在三角形ABC中,AB=AC,AD垂直于BC,垂足为点D,AN是三角形ABC外角角CAM 2020-06-27 …
如图,△ABC中,AB=6,BC=8,tan∠B=43,点D是边BC上的一个动点(点D与点B不重合 2020-07-20 …
已知:线段AB的长为L(1)线段AB上的点C满足关系式AC的平方=BC×AB,求线段AC的长度;( 2020-07-21 …
如图,已知等边△ABC,以边BC为直径的半圆与边AB,AC分别交于点D,点E,过点D作DF⊥AC, 2020-07-31 …
在Rt三角形ABC中,角B=90度,AC的垂直平分线交AC于点D,垂足点为E,已知,角CAD比角B 2020-08-01 …
如图,在平面直角坐标系中,点A(0,a),点B(b,0),点D(d,0),其中a、b、d满足|a-3 2020-11-03 …