早教吧作业答案频道 -->数学-->
如图,等边△ABC中,D是边BC上的一点,且BD:DC=1:3,把△ABC折叠,使点A落在边BC上的点D处,那么△BMD的面积△CDN的面积的值为.
题目详情
如图,等边△ABC中,D是边BC上的一点,且BD:DC=1:3,把△ABC折叠,使点A落在边BC上的点D处,那么
的值为___.
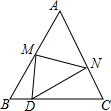
| △BMD的面积 |
| △CDN的面积 |

▼优质解答
答案和解析
∵BD:DC=1:3,
∴设BD=a,则CD=3a,
∵△ABC是等边三角形,
∴AB=BC=AC=4a,∠ABC=∠ACB=∠BAC=60°,
由折叠的性质可知:MN是线段AD的垂直平分线,
∴AM=DM,AN=DN,
∴BM+MD+BD=5a,DN+NC+DC=7a,
∵∠MDN=∠BAC=∠ABC=60°,
∴∠NDC+∠MDB=∠BMD+∠MBD=120°,
∴∠NDC=∠BMD,
∵∠ABC=∠ACB=60°,
∴△BMD∽△CDN,
∴(BM+MD+BD):(DN+NC+CD)=AM:AN,
即AM:AN=5:7,
∴MD:ND=5:7
∴
=(
)2=(
)=
,
故答案为:
.
∴设BD=a,则CD=3a,
∵△ABC是等边三角形,
∴AB=BC=AC=4a,∠ABC=∠ACB=∠BAC=60°,
由折叠的性质可知:MN是线段AD的垂直平分线,
∴AM=DM,AN=DN,
∴BM+MD+BD=5a,DN+NC+DC=7a,
∵∠MDN=∠BAC=∠ABC=60°,
∴∠NDC+∠MDB=∠BMD+∠MBD=120°,
∴∠NDC=∠BMD,
∵∠ABC=∠ACB=60°,
∴△BMD∽△CDN,
∴(BM+MD+BD):(DN+NC+CD)=AM:AN,
即AM:AN=5:7,
∴MD:ND=5:7
∴
| △BMD的面积 |
| △CDN的面积 |
| MD |
| ND |
| 5 |
| 7 |
| 25 |
| 49 |
故答案为:
| 25 |
| 49 |
看了 如图,等边△ABC中,D是边...的网友还看了以下:
已知a、b、c、d是非零实数,并满足a+b+c−dd=a+b−c+dc=a−b+c+db=−a+b 2020-05-13 …
在数学活动中,小明为了求1/2+1/2^2+1/2^3+.+1/2^2010的值,设计了如下图所示 2020-05-16 …
设向量AB=√2/2(a+5b),向量BC=-2a+8b,向量CD=3(a-b),则共线的三点是? 2020-07-03 …
如图,在O中,E是弧AB的中点,C为O上的一动点(C与E在AB异侧),连接EC交AB于点F,EB= 2020-07-29 …
如图,AB是圆圈O的直径,AB=10,DC切⊙O于C,DC切⊙O于点C,AD⊥DC,垂足为D,AD 2020-07-30 …
小明和小文同解方程组同解{ax+by=2小明正确解得{x=1小文因抄错c,解得{x=2cx+3y= 2020-07-31 …
如图:D在△ABE内部,点C在AE上,AD交BE于P,DC交BE于F,∠ABD=∠ACD,∠PDB= 2020-11-03 …
(2014•菏泽)如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD∥BC与过点A的切线交 2020-11-13 …
已知,c是ab上的一动点,(1)当c在线段ab上运动时,作dc⊥ab,垂足为C,EA⊥AB,垂足为A 2020-11-21 …
如图1,在⊙O中,E是弧AB的中点,C为⊙O上的一动点(C与E在AB异侧),连接EC交AB于点F,E 2020-12-03 …