如图，在平面直角坐标系中，点0是坐标原点．边长为6的正方形OABC的顶点A，C分别在x轴和y轴的正半轴上，点E是对角线AC上一点，连接OE、BE，BE的延长线交OA于点P，若△OCE的面积为12．（I）求

Question

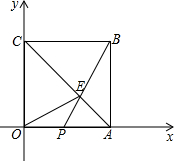
如图，在平面直角坐标系中，点0是坐标原点．边长为6的正方形OABC的顶点A，C分别在x轴和y轴的正半轴上，点E是对角线AC上一点，连接OE、BE，BE的延长线交OA于点P，若△OCE的面积为12．
（I）求点E的坐标：
（2）求△OPE的周长．

Answer 1

（1）过点E作EM⊥y轴于点M，

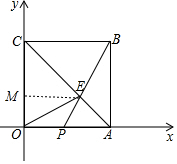
则(1)/(2)OC•EM=12，
即(1)/(2)×6×EM=12，
∴EM=4，
∵四边形OABC是正方形，
∴∠MCE=45°，
∴△MEC是等腰直角三角形，
∴MC=ME=4，
∴MO=6-4=2，
∴点E的坐标是（4，2）；

（2）设直线BE的解析式为y=kx+b，
把B（6，6）和点E（4，2）的坐标代入函数解析式得：

6k+b=6

4k+b=2

解得：k=2，b=-6，
∴直线BE的解析式为y=2x-6，
令2x-6=0得：x=3，
∴点P的坐标为（3，0），
∴OP=3，
∵四边形ABCO是正方形，
∴OC=CB，∠BCE=∠OCE，
在△OCE和△BCE中

OC=BC

∠OCE=∠BCE

CE=CE

∴△OCE≌△BCE（SAS），
∴OE=BE，
在Rt△PBA中，由勾股定理可得：PB=√(32+62)=3√(5)，
∴△OPE的周长=OE+PE+OP=3+PB=3+3√(5)．