早教吧作业答案频道 -->数学-->
如图①,在Rt△ABC中,∠ACB=90°,AC=BC,l是过点C的任意一条直线,过A作AD⊥l于D,过B作BE⊥l于E.(1)求证:△ACD≌△ACD;(2)如图②延长BE至F,连接CF,以CF为直角边作等腰Rt△FCG,∠FCG=90°
题目详情
如图①,在Rt△ABC中,∠ACB=90°,AC=BC,l是过点C的任意一条直线,过A作AD⊥l于D,过B作BE⊥l于E.
(1)求证:△ACD≌△ACD;
(2)如图②延长BE至F,连接CF,以CF为直角边作等腰Rt△FCG,∠FCG=90°,连接AG交l于H.求证:BF=2CH.
(3)在(2)的条件下,若AD=12,BE=15,BC=13,请直接写出点G到直线AC的距离.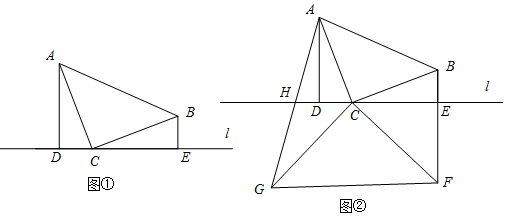
(1)求证:△ACD≌△ACD;
(2)如图②延长BE至F,连接CF,以CF为直角边作等腰Rt△FCG,∠FCG=90°,连接AG交l于H.求证:BF=2CH.
(3)在(2)的条件下,若AD=12,BE=15,BC=13,请直接写出点G到直线AC的距离.

▼优质解答
答案和解析
(1)证明:如图①中,
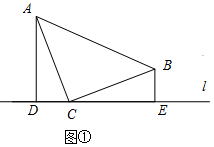
∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=∠ACB=90°,
∵∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS).
(2)如图②中,作AM∥CG交EH于M,连接GM.
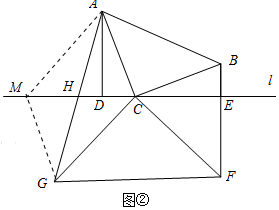
∵∠MAC+∠ACG=180°,∠ACG+∠BCF=180°,
∴∠MAC=∠BCF,
∵∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACM=∠CBF,
在△ACM和△CBF中,
,
∴△MAC≌△CBF,
∴CM=BF,AM=CF=CG,∵AM∥CG,
∴四边形AMGC是平行四边形,
∴MH=HC,
∴BF=CM=2CH.
(3)∵△MAC≌△CBF,
∴CM=BF=15,
∵AC=BC=13,
∴S四边形AMCG=2•S△AMC=AC•h(h是点G到AC的距离),
∴2×
×15×12=13h,
∴h=

∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=∠ACB=90°,
∵∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
|
∴△ADC≌△CEB(AAS).
(2)如图②中,作AM∥CG交EH于M,连接GM.

∵∠MAC+∠ACG=180°,∠ACG+∠BCF=180°,
∴∠MAC=∠BCF,
∵∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACM=∠CBF,
在△ACM和△CBF中,
|
∴△MAC≌△CBF,
∴CM=BF,AM=CF=CG,∵AM∥CG,
∴四边形AMGC是平行四边形,
∴MH=HC,
∴BF=CM=2CH.
(3)∵△MAC≌△CBF,
∴CM=BF=15,
∵AC=BC=13,
∴S四边形AMCG=2•S△AMC=AC•h(h是点G到AC的距离),
∴2×
| 1 |
| 2 |
∴h=
| 180 |
| 13 |
看了 如图①,在Rt△ABC中,∠...的网友还看了以下:
(2014•吴中区一模)已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙ 2020-05-17 …
平面直角坐标系的一道题,读不懂...在方格纸上建立平面直角坐标系,并描出下列各点:A(1,1)B( 2020-06-03 …
关于瞬时加速度质量比为1:2:3的A,B,C三个钩码在外力F的作用下以加速度g竖直向上做匀加速直线 2020-06-04 …
点C是半圆O半径OB上动点,做PC垂直AB于C,D是半圆上位于PC左侧的点,连结BD交PC于E点C 2020-07-17 …
如图,AB是O的直径,C是弧AB的中点,连接AC并延长至D,使DC=CA,连接DB,点E为OB的中 2020-07-21 …
已知,如图,AB是⊙O的直径,C是⊙O上一点,连接AC,过点C作直线CD⊥AB于D(AD<DB), 2020-07-22 …
下列有关心脏的说法,正确的是()A.左心房与右心室直接相连通B.左心房与右心房直接相连通C.左心室 2020-07-29 …
下列有关心脏的说法,正确的是()A.左心房与右心室直接相连通B.左心房与右心房直接相连通C.左心室 2020-07-29 …
如图,AB为O的直径,C为O上一点,AD和过点C的切线互相垂直,垂足为D,AD交O于点E(1)求证 2020-07-30 …
一台服务器分别与一台笔记本电脑和一台交换机的网口连接分别用什么网线。A.交叉线/交叉线B.直连线/ 2020-08-01 …