早教吧作业答案频道 -->数学-->
我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△
题目详情
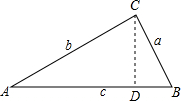
我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA
∴BD=c-bcosA
在Rt△BDC中,由勾股定理:CD2+BD2=BC2
(c-bcosA)2+(bsinA)2=a2,整理得:a2=b2+c2-2bccosA
同理可得:b2=a2+c2-2accosB,c2=a2+b2-2abcosC.
利用上述结论解答下列问题:
(1)锐角在△ABC中,∠A=45°,b=2
,c=2,求a和∠C的大小
(2)在△ABC中,a=
,b=
,∠B=45°,(c>a>b),求边长c的长度.
∴BD=c-bcosA
在Rt△BDC中,由勾股定理:CD2+BD2=BC2
(c-bcosA)2+(bsinA)2=a2,整理得:a2=b2+c2-2bccosA
同理可得:b2=a2+c2-2accosB,c2=a2+b2-2abcosC.
利用上述结论解答下列问题:

(1)锐角在△ABC中,∠A=45°,b=2
| 2 |
(2)在△ABC中,a=
| 3 |
| 2 |
▼优质解答
答案和解析
(1)在锐角△ABC中,a2=b2+c2-2bccosA
=(2
)2+4-2×2
×2×
=4
解得,a=2,
22+22=(2
)2
∴△ABC为直角三角形,a=c=2,
∴∠C=45°;
(2)∵b2=a2+c2-2accosB,
∴c2-
c+1=0,
解得,c=
,
∵c>a>b,
∴c=
.
=(2
| 2 |
| 2 |
| ||
| 2 |
=4
解得,a=2,
22+22=(2
| 2 |
∴△ABC为直角三角形,a=c=2,
∴∠C=45°;
(2)∵b2=a2+c2-2accosB,
∴c2-
| 6 |
解得,c=
| ||||
| 2 |
∵c>a>b,
∴c=
| ||||
| 2 |
看了 我们知道,直角三角形的边角关...的网友还看了以下:
已知函数y=f(x)在t=0处可导,且具有性质f(t+s)=(f(t)+f(s))/(1-f(t) 2020-06-08 …
已知二次函数f(x)=x^2-16x+q+3.1.若函数在区间[-1,1]上存在零点,求实数q的取 2020-06-12 …
已知二次函数f(x)=x^2-16x+q+3 (1)若函数在区间〔-1,1〕上存在零点,求实数q的 2020-06-27 …
若存在t∈R与正数m,使F(t-m)=F(t+m)成立,则称“函数F(x)在x=t处存在距离为2m 2020-07-26 …
(12分)已知二次函数。(1)若函数在区间[-1,1]上存在零点,求实数q的取值范围;(2)问是否存 2020-11-01 …
平面向量问题已知平面向量a=(√3/2,-1/2),b=(1/2,√3/2)若存在不同时为零的实数k 2020-11-02 …
已知勾函数……求实数t的取值范围.已知勾函数y=x+a∧2/x(a>0)在(-∞,-a)和(a,+∞ 2020-11-08 …
函数fx的定义域为D,若满足1fx在D内是单调函数2存在a/2,b/2属于D,使得fx的值域为a,b 2020-12-09 …
服药后,人体血液中药物的质量浓度y是时间t的函数y=f(t).假设函数y=f(t)在t=10和t=1 2020-12-22 …
函数f(x)的定义域为D,若满足如下两条件:①f(x)在D内是单调函数;②存在[m2,n2]⊆D,使 2021-01-04 …