早教吧作业答案频道 -->数学-->
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:①PA+PB+PC+PD的最小值为10;②若△PAB≌△PCD,则△PAD≌△PBC
题目详情
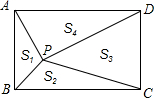
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:
①PA+PB+PC+PD的最小值为10;
②若△PAB≌△PCD,则△PAD≌△PBC;
③若S1=S2,则S3=S4,
④若△PAB~△PDA,则PA=2.4
其中正确的是___(把所有正确的结论的序号都填在横线上)
①PA+PB+PC+PD的最小值为10;
②若△PAB≌△PCD,则△PAD≌△PBC;
③若S1=S2,则S3=S4,
④若△PAB~△PDA,则PA=2.4
其中正确的是___(把所有正确的结论的序号都填在横线上)

▼优质解答
答案和解析
①当点P是矩形ABCD两对角线的交点时,PA+PB+PC+PD的值最小,根据勾股定理得,AC=BD=5,所以PA+PB+PC+PD的最小值为10,故①正确;
②若△PAB≌△PCD,则PA=PC,PB=PD,所以P在线段AC、BD的垂直平分线上,即P是矩形ABCD两对角线的交点,所以△PAD≌△PBC,故②正确;
③若S1=S2,易证S1+S3=S2+S4,则S3=S4,故③正确;
④若△PAB~△PDA,则∠PAB=∠PDA,∠PAB+∠PAD=∠PDA+∠PAD=90°,∠APD=180°-(∠PDA+∠PAD)=90°,同理可得∠APB=90°,那么∠BPD=180°,B、P、D三点共线,P是直角△BAD斜边上的高,根据面积公式可得PA=2.4,故④正确.
故答案为①②③④.
②若△PAB≌△PCD,则PA=PC,PB=PD,所以P在线段AC、BD的垂直平分线上,即P是矩形ABCD两对角线的交点,所以△PAD≌△PBC,故②正确;
③若S1=S2,易证S1+S3=S2+S4,则S3=S4,故③正确;
④若△PAB~△PDA,则∠PAB=∠PDA,∠PAB+∠PAD=∠PDA+∠PAD=90°,∠APD=180°-(∠PDA+∠PAD)=90°,同理可得∠APB=90°,那么∠BPD=180°,B、P、D三点共线,P是直角△BAD斜边上的高,根据面积公式可得PA=2.4,故④正确.
故答案为①②③④.
看了 如图,点P是矩形ABCD内一...的网友还看了以下:
△ABC是边长为4的等边三角形,BC在X轴上,点D为BC的中点点A在第一象限内,AB与Y轴的正半轴 2020-05-13 …
求助一个关于C语言指针的问题int main(){x09int a[]={1,2,3,4,5};x 2020-05-13 …
设服从二项分布B~(n,p)的随机变量ξ的期望和方差分别是2.4与1.44,则二项分布的参数n、p 2020-05-15 …
在正确的读音后打“√”。1.少年回到自己的铺(pūpù)位,躺了下来,拉上了帘子。2.海参(shē 2020-05-16 …
请高手帮解决下面几何题,在正方体ABCD-A/B/C/D中,P是线段B/C上一个动点,下列命题错误 2020-05-19 …
经过下列语句intj,a[10],*p;定义后,下列语句合法的是()A.p=p+2B.p=经过下列语 2020-11-06 …
某种商品的市场价格P随市场变化自动调节,设需求函数为D(p)=4-p^2,供给函数为S(p)=2p+ 2020-11-17 …
某种商品的市场价格P随市场变化自动调节,设需求函数为D(p)=4-p^2,供给函数为S(p)=2p+ 2020-11-17 …
点P为直线L外一点,点A、B、C为直线L上的三点,并且PA=5CM,pb=4CM,PC=3CM,则点 2020-11-23 …
求你们了!真的不会!谁会,大大地有赏设f(x)=x^2+px+q,g(x)=x^2+qx+p,p、q 2020-12-31 …