早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.(1)求抛物线的函数表达式;(2)是否存在点P,使得△ACP是以AC为底边的等
题目详情
如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
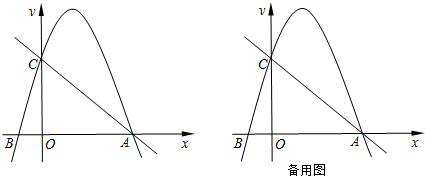
(1)求抛物线的函数表达式;
(2)是否存在点P,使得△ACP是以AC为底边的等腰三角形?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q为线段AC上一点,若四边形OCPQ为平行四边形,求点Q的坐标.

(1)求抛物线的函数表达式;
(2)是否存在点P,使得△ACP是以AC为底边的等腰三角形?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q为线段AC上一点,若四边形OCPQ为平行四边形,求点Q的坐标.
▼优质解答
答案和解析
(1)∵C (0,4),
∴OC=4.
∵OA=OC=4OB,
∴OA=4,OB=1,
∴A (4,0),B (-1,0),
设抛物线解析式:y=a(x+1)(x-4),
∴4=-4a,
∴a=-1.
∴y=-x2+3x+4.
(2)存在.
若△ACP是以AC为底的等腰三角形,则点P在AC的垂直平分线上,
∵OA=OC,
∴AC的垂直平分线OP即为∠AOC的平分线,
设P(m,-m2+3m+4),
则可得:m=-m2+3m+4,
∴m1=
+1,m2=1-
∴存在点P1(
+1,
+1),P2(1-
,1-
),使得△ACP是以AC为底边的等腰三角形.
(3)设lAC:y=kx+b(k≠0),
∵过A (4,0),C (0,4),
∴lAC:y=-x+4.
∵四边形OCPQ为平行四边形,
∴PQ∥OC,PQ=OC,
设P(t,-t2+3t+4),Q(t,-t+4),
-t2+3t+4-(-t+4)=4.
∴t1=t2=2,
∴点Q(2,2).
∴OC=4.
∵OA=OC=4OB,
∴OA=4,OB=1,
∴A (4,0),B (-1,0),
设抛物线解析式:y=a(x+1)(x-4),
∴4=-4a,
∴a=-1.
∴y=-x2+3x+4.
(2)存在.
若△ACP是以AC为底的等腰三角形,则点P在AC的垂直平分线上,
∵OA=OC,
∴AC的垂直平分线OP即为∠AOC的平分线,
设P(m,-m2+3m+4),
则可得:m=-m2+3m+4,
∴m1=
| 5 |
| 5 |
∴存在点P1(
| 5 |
| 5 |
| 5 |
| 5 |
(3)设lAC:y=kx+b(k≠0),
∵过A (4,0),C (0,4),
∴lAC:y=-x+4.
∵四边形OCPQ为平行四边形,
∴PQ∥OC,PQ=OC,
设P(t,-t2+3t+4),Q(t,-t+4),
-t2+3t+4-(-t+4)=4.
∴t1=t2=2,
∴点Q(2,2).
看了 如图,在平面直角坐标系中,已...的网友还看了以下:
三角形三边长满足以下几个关系式:b=a−3+3−a+4,c是a2+b2的算术平方根,试求三角形三边 2020-05-13 …
已知inta[4][5],则对数组a的元素引用正确的是()A.a[0][4]B.a[4][5]C. 2020-06-03 …
a²-4(a+b)²有一个因式是a+2b+2c,则另一个因式是请写出2的64次方-1的两个因数第一 2020-06-03 …
如图,数轴上点A、C对应的数分别为a,c,且a,c满足|a+4|+(c-1)2014=0,点B对应 2020-06-13 …
因式分解:a^4(b-c)+b^4(c-a)+c^4(a-b)完整答案! 2020-07-20 …
如图,数轴上点A,C对应的数分布是a,c,且a,c满足|a+4|+(c-1)2=0,点B对应的数是 2020-07-22 …
如图,数轴上点A、C对应的数分别为a、c,且a、c满足|a+4|+(c-1)2=0.,点B对应的数 2020-07-30 …
如图,数轴上点A、C对应的数分别为a、c,且a、c,满足|a+4|+(c-1)2014=0,点O对 2020-07-30 …
1.分解a²-a-12的结果为()A.(a-3)(a+4)B.(a+3)(a-4)C.(a-6)( 2020-08-03 …
在等腰三角形ABC中,三边分别为a,b,c,其中a=4,b,c恰好是方程x平方-(2k+1)x+4( 2020-11-10 …