早教吧作业答案频道 -->数学-->
△ABC是等边三角形,以点C为旋转中心,将线段CA按顺时针方向旋转60°得到线段CD,连接BD交AC于点O.(1)如图1.①求证:AC垂直平分BD;①点M在BC的延长线上,点N在线段CO上,且ND=NM,连接BN
题目详情
△ABC是等边三角形,以点C为旋转中心,将线段CA按顺时针方向旋转60°得到线段CD,连接BD交AC于点O.
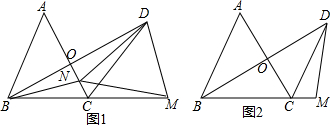
(1)如图1.
①求证:AC垂直平分BD;
①点M在BC的延长线上,点N在线段CO上,且ND=NM,连接BN,判断△MND的形状,并加以证明;
(2)如图2,点M在BC的延长线上,点N在线段AO上,且ND=NM,补全图2,求证:NA=MC.

(1)如图1.
①求证:AC垂直平分BD;
①点M在BC的延长线上,点N在线段CO上,且ND=NM,连接BN,判断△MND的形状,并加以证明;
(2)如图2,点M在BC的延长线上,点N在线段AO上,且ND=NM,补全图2,求证:NA=MC.
▼优质解答
答案和解析
证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠CAB=60°,
①以点C为旋转中心,将线段CA按顺时针方向旋转60°得到线段CD,
∴CD=CA,∠ACD=∠ACB=60°,
∴BO=DO,CO⊥BD,
∴AC垂直平分BD;
②△MND是等边三角形,
如图1,由①知AC垂直平分BD,
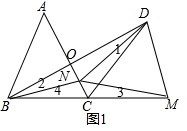
∴NB=ND,∠CBD=
∠ABC=30°,
∴∠1=∠2,
∴∠BND=180°-2∠2,
∵ND=NM,
∴NB=NM,
∴∠3=∠4,∠BNM=180°-2∠4,
∴∠DNM=360°-180°+2∠2-180°+2∠4=2(∠2+∠4)=60°,
∴△MND是等边三角形;
(2)连接AD,BN,如图2,
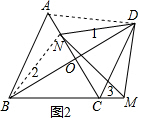
由题意知,△ACD是等边三角形,
∴∠ADC=60°,AD=CD,
与(1)同理可证∠1=∠2,∠3=∠NBM,
∠BND=180°-2∠2,∠BNM=180°-2∠NBM,
∴∠MND=∠BND-∠BNM=2(∠NBM-∠2)=60°,
∵ND=NM,
∴△MND是等边三角形,
∴DN=DM,∠NDM=60°,∠ADC=∠NDM,
∴∠NDA=∠MDC,
在△AND与△MDC中
,
∴△AND≌△CMD,
∴NA=MC.
∴∠ABC=∠ACB=∠CAB=60°,
①以点C为旋转中心,将线段CA按顺时针方向旋转60°得到线段CD,
∴CD=CA,∠ACD=∠ACB=60°,
∴BO=DO,CO⊥BD,
∴AC垂直平分BD;
②△MND是等边三角形,
如图1,由①知AC垂直平分BD,

∴NB=ND,∠CBD=
| 1 |
| 2 |
∴∠1=∠2,
∴∠BND=180°-2∠2,
∵ND=NM,
∴NB=NM,
∴∠3=∠4,∠BNM=180°-2∠4,
∴∠DNM=360°-180°+2∠2-180°+2∠4=2(∠2+∠4)=60°,
∴△MND是等边三角形;
(2)连接AD,BN,如图2,

由题意知,△ACD是等边三角形,
∴∠ADC=60°,AD=CD,
与(1)同理可证∠1=∠2,∠3=∠NBM,
∠BND=180°-2∠2,∠BNM=180°-2∠NBM,
∴∠MND=∠BND-∠BNM=2(∠NBM-∠2)=60°,
∵ND=NM,
∴△MND是等边三角形,
∴DN=DM,∠NDM=60°,∠ADC=∠NDM,
∴∠NDA=∠MDC,
在△AND与△MDC中
|
∴△AND≌△CMD,
∴NA=MC.
看了 △ABC是等边三角形,以点C...的网友还看了以下:
如图,在平行四边形ABCD中,AD=2AB=6cm,BE是∠ABC的角平分线,点M从点E出发,沿E 2020-05-13 …
(可能有点难,在一个直角梯形中,有一条线交上底AD于点M,下底BC于N.AD//BC,角B=90度 2020-05-20 …
解析几何关于面积最值问题在平面直角坐标系xOy中,过定点C(o,p)作直线与抛物线x^2=2py( 2020-06-03 …
几何题直角梯形已知在直角梯形ABCD中,AD//BC,角B=角A=90°,BC=CD=10,AB: 2020-06-04 …
如图,等边△ABC的边长为8,动点M从点B出发,沿B→A→C→B的方向以3cm/s的速度运动,动点 2020-06-12 …
在△ABC中,∠ACB=90°,AC=BC,AB=8,CD⊥AB,垂足为D,M为边AB上任意一点, 2020-06-12 …
如图,平面直角坐标系中,直角梯形OABC的点O在坐标原点B(15,8),C(21,0),动点M从点 2020-06-13 …
在平面直角坐标系xOy中,过定点C(0,p)作直线与抛物线x2=2py(p>0)相交于A、B两点。 2020-07-19 …
如图,等边△ABC的边长为8cm,动点M从点B出发,沿B到A到C到B的方向以3cm/s的速度运动, 2020-07-26 …
在平面直角坐标系xoy中,过定点c(0,p)作直线与抛物线y^2=2py(p>0)交于a,b两点, 2020-08-02 …