早教吧作业答案频道 -->数学-->
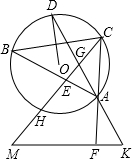
已知,如图,O是△ABC的外接圆,OD⊥BC交O于点D,CE平分∠ACB交AB于点E,交O于点H,AD与CH相交于点G,延长CH到点M,使MH=HG,延长DA到点K,使AK=AG,CA的延长线交MK于点F,求证:ME=MF.
题目详情
已知,如图, O是△ABC的外接圆,OD⊥BC交 O于点D,CE平分∠ACB交AB于点E,交 O于点H,AD与CH相交于点G,延长CH到点M,使MH=HG,延长DA到点K,使AK=AG,CA的延长线交MK于点F,求证:ME=MF.

▼优质解答
答案和解析
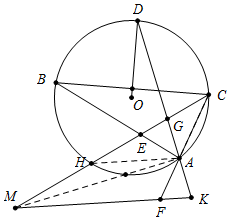
证明:如图,连接AH、AM.
∵OD⊥BC,
∴
=
,
∴∠BAD=∠CAD,
∵∠BCH=∠ACH,∠BCH=∠BAH,
∴∠BAH=∠ACH,
∵∠HGA=∠ACH+∠CAG,∠HAG=∠BAH+∠BAD,
∴∠HGA=∠HAG,
∴HA=GH=HM,
∴△MAG是直角三角形,
∴MA⊥KG,
∵AG=AK,
∴MG=MK,
∴∠AGE=∠K,
∵∠FAK=∠CAD,∠BAD=∠DAC,
∴∠EAG=∠FAK,
在△AGE和△AKF中,
,
∴△AGE≌△AKF,
∴EG=FK,∵MG=MK,
∴ME=MF.

∵OD⊥BC,
∴
 |
| DB |
 |
| DC |
∴∠BAD=∠CAD,
∵∠BCH=∠ACH,∠BCH=∠BAH,
∴∠BAH=∠ACH,
∵∠HGA=∠ACH+∠CAG,∠HAG=∠BAH+∠BAD,
∴∠HGA=∠HAG,
∴HA=GH=HM,
∴△MAG是直角三角形,
∴MA⊥KG,
∵AG=AK,
∴MG=MK,
∴∠AGE=∠K,
∵∠FAK=∠CAD,∠BAD=∠DAC,
∴∠EAG=∠FAK,
在△AGE和△AKF中,
|
∴△AGE≌△AKF,
∴EG=FK,∵MG=MK,
∴ME=MF.
看了 已知,如图,O是△ABC的外...的网友还看了以下:
比例线段的简单问题.已知:a分之b=d分之c,求证:b分之(b-a)=d分之(d-c) 2020-05-21 …
如图,长方体OABC-D'A'B'C'中,|OA|=3,|OC|=4,|OD'|=3,A'C'于B 2020-06-14 …
b分之a=d分之c=3b+d≠0则b+d分之a+c=?过程详细谢谢 2020-06-17 …
如果b分之a=d分之c,那么b分之a+b=d分之c+d,b分之a-b=d分之c-你认为这个结论正确 2020-07-14 …
b分之a=d分之c=f分之e=3分之2求(1)b+d分之a+c(2)2b-d+3f分之2a-c+3 2020-07-20 …
设A为n(n≥2)阶可逆矩阵,交换A的第1行与第2行得矩阵B,A*,B*分别为A,B的伴随矩阵,则 2020-07-22 …
如图,如图矩形abcd中,把∠b,∠d分别翻折,使点b,d恰好落在对角线ac上的点e,f处,折,使 2020-07-22 …
若b分之a=c分之b=d分之c=a分之d,则a+b-c+d分之a-b+c-d 2020-07-29 …
比例线段如果b分之a=d分之c=k(k为常数),那么b分之a+b=d分之c+d成立吗,为什么? 2020-08-02 …
三角形ABC相似三角形A'B'C',BD和B'D'是它们地对应中线,已知AC/A'C'=3/2,B 2020-08-03 …