早教吧作业答案频道 -->数学-->
如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.(Ⅰ)证明:B,C,G,F四点共圆;(Ⅱ)若AB=1,E为DA的中点,求四边形BCGF的面积.
题目详情
如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.
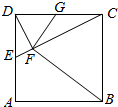
(Ⅰ)证明:B,C,G,F四点共圆;
(Ⅱ)若AB=1,E为DA的中点,求四边形BCGF的面积.

(Ⅰ)证明:B,C,G,F四点共圆;
(Ⅱ)若AB=1,E为DA的中点,求四边形BCGF的面积.
▼优质解答
答案和解析
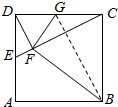 (Ⅰ)证明:∵DF⊥CE,
(Ⅰ)证明:∵DF⊥CE,
∴Rt△DFC∽Rt△EDC,
∴
=
,
∵DE=DG,CD=BC,
∴
=
,
又∵∠GDF=∠DEF=∠BCF,
∴△GDF∽△BCF,
∴∠CFB=∠DFG,
∴∠GFB=∠GFC+∠CFB=∠GFC+∠DFG=∠DFC=90°,
∴∠GFB+∠GCB=180°,
∴B,C,G,F四点共圆.
(Ⅱ)∵E为AD中点,AB=1,∴DG=CG=DE=
,
∴在Rt△DFC中,GF=
CD=GC,连接GB,Rt△BCG≌Rt△BFG,
∴S四边形BCGF=2S△BCG=2×
×1×
=
.
 (Ⅰ)证明:∵DF⊥CE,
(Ⅰ)证明:∵DF⊥CE,∴Rt△DFC∽Rt△EDC,
∴
| DF |
| ED |
| CF |
| CD |
∵DE=DG,CD=BC,
∴
| DF |
| DG |
| CF |
| BC |
又∵∠GDF=∠DEF=∠BCF,
∴△GDF∽△BCF,
∴∠CFB=∠DFG,
∴∠GFB=∠GFC+∠CFB=∠GFC+∠DFG=∠DFC=90°,
∴∠GFB+∠GCB=180°,
∴B,C,G,F四点共圆.
(Ⅱ)∵E为AD中点,AB=1,∴DG=CG=DE=
| 1 |
| 2 |
∴在Rt△DFC中,GF=
| 1 |
| 2 |
∴S四边形BCGF=2S△BCG=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
看了 如图,在正方形ABCD中,E...的网友还看了以下:
如图,将一张矩形纸片ABCD沿EF折叠,使顶点C,D分别落在点C’,D’处,C’E交AF于点G.若 2020-05-13 …
在矩形ABCD中,点E是边CD的中点,将三角形ADE沿AE折叠后得到三角形AFE,点F在矩形ABC 2020-05-16 …
如图,在平行四边形ABCD中,若设BA向量=a向量,BD的向量=b向量,则有BE向量=1/4a,B 2020-05-16 …
判断化学平衡,对于有固体或者液体的物质参与的反应,如aA(s)+bB(g)cC(g)+dD(g); 2020-06-14 …
如图,在△ABC中,∠BAC的平分线交BC于点D.(1)如图1,若∠B=62°,∠C=38°,AE 2020-06-23 …
如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折 2020-06-24 …
BE平分∠ABD,CF平分∠ACD,BE与CF相交于点G,若∠BDC=140°,∠BGC=100° 2020-07-16 …
如图,已知AB是○O的直径,CD与○O相切与点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于 2020-11-26 …
在Rt三角形ABC中,角ACB=90°,CA=CB,D为BC边的中点,DE垂直AB于E,过点B作BF 2020-12-01 …
如图,梯形ABCD中,AD//BC,点E是边AD的中点,连结BE交AC于点F,BE的延长线交CD的延 2021-01-02 …