早教吧作业答案频道 -->数学-->
如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且A1A⊥底面ABCD,点P、Q分别在棱DD1,BC上,BQ=4.(1)若DP=23DD1,证明:PQ∥平面ABB1A1;(2)若P是D1D的中点,证明
题目详情
如图,已知四棱台ABCD-A1B1C1D1的上、下底面分别是边长为3和6的正方形,AA1=6,且A1A⊥底面ABCD,点P、Q分别在棱DD1,BC上,BQ=4.
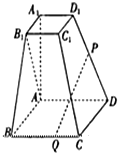
(1)若DP=
DD1,证明:PQ∥平面ABB1A1;
(2)若P是D1D的中点,证明:AB1⊥平面PBC.

(1)若DP=
| 2 |
| 3 |
(2)若P是D1D的中点,证明:AB1⊥平面PBC.
▼优质解答
答案和解析
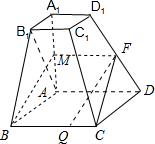 证明:(1)在AA1上取一点N,使得AN=
证明:(1)在AA1上取一点N,使得AN=
AA1,
∵DP=
DD1,且A1D1=3,AD=6,
∴PN
AD,又BQ
AD,
∴PN
BQ,
∴四边形BQPN为平行四边形,
∴PQ∥BN,
∵BN⊂平面ABB1A1,PQ⊄ABB1A1.
∴PQ∥ABB1A1.…6分
(2)如图所示,取A1A的中点M,连接PM,BM,PC,
∵A1,A,D1D是梯形的两腰,P是D1D的中点,
∴PM∥AD,于是由AD∥BC知,PM∥BC,
∴P,M,B,C四点共面,
由题设可知,BC⊥AB,BC⊥A1A,
∴BC⊥平面ABB1A1,
∴BC⊥AB1,①
∵tan∠ABM=
=
=
=tan∠A1AB1,
∴∠ABM=∠A1AB1,
∴∠ABM+∠BAB1=∠A1AB1+∠BAB1=90°,
∴AB1⊥BM,
再由①与BC∩BM=B,知AB1⊥平面PBC.…12分
 证明:(1)在AA1上取一点N,使得AN=
证明:(1)在AA1上取一点N,使得AN=| 2 |
| 3 |
∵DP=
| 2 |
| 3 |
∴PN
| ∥ |
. |
| 2 |
| 3 |
| ∥ |
. |
| 2 |
| 3 |
∴PN
| ∥ |
. |
∴四边形BQPN为平行四边形,
∴PQ∥BN,
∵BN⊂平面ABB1A1,PQ⊄ABB1A1.
∴PQ∥ABB1A1.…6分
(2)如图所示,取A1A的中点M,连接PM,BM,PC,
∵A1,A,D1D是梯形的两腰,P是D1D的中点,
∴PM∥AD,于是由AD∥BC知,PM∥BC,
∴P,M,B,C四点共面,
由题设可知,BC⊥AB,BC⊥A1A,
∴BC⊥平面ABB1A1,
∴BC⊥AB1,①
∵tan∠ABM=
| AM |
| AB |
| 3 |
| 6 |
| A1B1 |
| A1A |
∴∠ABM=∠A1AB1,
∴∠ABM+∠BAB1=∠A1AB1+∠BAB1=90°,
∴AB1⊥BM,
再由①与BC∩BM=B,知AB1⊥平面PBC.…12分
看了 如图,已知四棱台ABCD-A...的网友还看了以下:
(1)若a,b,c为三角形的三边长,试证明:(a^2+b^2-b^2)^2-4a^2*b^2一定为负 2020-03-30 …
设A是n阶矩阵(n≥2),试证 R(A*)=n若R(A)=n,=1若R(A)=n-1 =0若R(设 2020-04-05 …
数集A满足条件若a∈A则有(1+a)/(1-a)∈A(a≠1)数集A满足条件若a∈A则有(1+a) 2020-04-05 …
如图1所示是用U形管压强计研究液体内部压强规律的示意图,图中探究的是液体内部压强与的关系.图2是“ 2020-05-13 …
已知AB∥CD,探究下列几种情况:(1)如图1,若∠EAF=12∠EAB,∠ECF=12∠ECD, 2020-05-23 …
在四边形ABCD中,∠A=∠BCD=9(1)过点C做对角线BD的垂线,分别交BD、AD于点E、F. 2020-06-06 …
若集合M={x丨-3≤x≤4},集合P={x丨2m-1≤x≤m+1}.(1)证明:M与P不可能相等 2020-06-12 …
在四边形ABCD中AB=AD,AC于BD交于点E,∠ADB=∠ACB.(1)求证AB/AE=AC/ 2020-06-12 …
已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.(1)如图1,若点O在边BC 2020-06-12 …
1.设A是3阶实对称矩阵,若A^2=0,证明A=0问一下用相似对角化怎么证?2.若证矩阵为零,让其 2020-06-22 …