早教吧作业答案频道 -->数学-->
如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.(1)求证:DQ=PQ;(2)求AP•DQ的最大值;(3)若P为AB的中点,求PG的长.
题目详情
如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
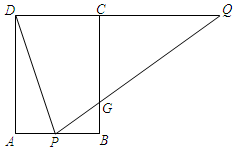
(1)求证:DQ=PQ;
(2)求AP•DQ的最大值;
(3)若P为AB的中点,求PG的长.

(1)求证:DQ=PQ;
(2)求AP•DQ的最大值;
(3)若P为AB的中点,求PG的长.
▼优质解答
答案和解析
 (1)证明:∵四边形ABDF是矩形,
(1)证明:∵四边形ABDF是矩形,
∴AB∥CD,
∴∠APD=∠QDP.
∵∠APD=∠QPD,
∴∠QPD=∠QDP,
∴DQ=PQ.
(2)过点Q作QE⊥DP,垂足为E,则DE=
DP.
∵∠DEQ=∠PAD=90°,∠QDP=∠APD,
∴△QDE∽△DPA,
∴
=
,
∴AP•DQ=DP•DE=
DP2.
在Rt△DAP中,有DP2=DA2+AP2=36+AP2,
∴AP•DQ=
(36+AP2),
∵点P在AB上,
∴AP≤4,
∴AP•DQ≤26,即AP•DQ的最大值为26.
(3)∵P为AB的中点,
∴AP=BP=
AB=2,
由(2)得,DQ=
(36+22)=10.
∴CQ=DQ-DC=6.设CG=x,则BG=6-x,
由(1)得,DQ∥AB,
∴
=
,
即
=
,
解得x=
,
∴BG=6-
=
,
∴PG=
=
.
 (1)证明:∵四边形ABDF是矩形,
(1)证明:∵四边形ABDF是矩形,∴AB∥CD,
∴∠APD=∠QDP.
∵∠APD=∠QPD,
∴∠QPD=∠QDP,
∴DQ=PQ.
(2)过点Q作QE⊥DP,垂足为E,则DE=
| 1 |
| 2 |
∵∠DEQ=∠PAD=90°,∠QDP=∠APD,
∴△QDE∽△DPA,
∴
| DQ |
| DP |
| DE |
| AP |
∴AP•DQ=DP•DE=
| 1 |
| 2 |
在Rt△DAP中,有DP2=DA2+AP2=36+AP2,
∴AP•DQ=
| 1 |
| 2 |
∵点P在AB上,
∴AP≤4,
∴AP•DQ≤26,即AP•DQ的最大值为26.
(3)∵P为AB的中点,
∴AP=BP=
| 1 |
| 2 |
由(2)得,DQ=
| 1 |
| 4 |
∴CQ=DQ-DC=6.设CG=x,则BG=6-x,
由(1)得,DQ∥AB,
∴
| CQ |
| BP |
| CG |
| BG |
即
| 6 |
| 2 |
| x |
| 6-x |
解得x=
| 9 |
| 2 |
∴BG=6-
| 9 |
| 2 |
| 3 |
| 2 |
∴PG=
| PB2+BG2 |
| 5 |
| 2 |
看了 如图,矩形ABCD中,AB=...的网友还看了以下:
为啥任何一组勾股数必定可以表示为a=p^2-q^2,b=2pq,c=p^2+q^2p、q(q 2020-05-13 …
抛物线Y^2=2px(p>0)上一点M到焦点的距离为a(a大于等于2p),求点M到Y轴的最短距离是 2020-05-13 …
对于有理数a、b,定义运算:“⊗”,a⊗b=ab-a-b-2.(1)计算:(-2)⊗3的值;(2) 2020-06-06 …
已知函数f(x)对于任意实数a,b满足f(ab)=f(a)+f(b),且f(2)=p,f(3)=q 2020-07-19 …
inta[2][3]={1,2,3,4,5,6},(*p)[3]=a,则下列哪个表达式不是3?为什 2020-07-20 …
p在数轴上的位置如图所示,化简:|p-1|+|p-2|=. 2020-07-30 …
指针问题设intx[]={1,2,3,4,5,6},*p=x;则数值为3的表达式是(B)。(A)p 2020-07-30 …
说出下面不等式的变形是根据不等式的哪一个基本性质.(1)如果3a<6,那么a<2.(2)如果a-3 2020-08-03 …
()1.A.p()2.A.r()3.A.RI()4.A.Mr()5.A.()6.A.()7.A.tw 2020-10-30 …
递回关系式的运算公式(数列)以下是推导一个公式"a=a+r(1-p^n)/(1-p)"的过程a=p* 2021-01-13 …