早教吧作业答案频道 -->数学-->
已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;(2)如图2,若点P在线段AB的中点,
题目详情
已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.
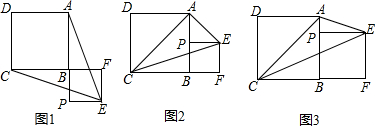
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(3)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.

(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(3)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.
▼优质解答
答案和解析
证明:(1)∵四边形ABCD和四边形BPEF是正方形,
∴AB=BC,BP=BF,
∴AP=CF,
在△APE和△CFE中,
∵
,
∴△APE≌△CFE,
∴EA=EC;
(2)△ACE是直角三角形,理由是:
如图2,∵P为AB的中点,
∴PA=PB,
∵PB=PE,
∴PA=PE,
∴∠PAE=45°,
又∵∠BAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
(3)设CE交AB于G,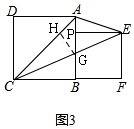
∵EP平分∠AEC,EP⊥AG,
∴AP=PG=a-b,BG=a-(2a-2b)=2b-a,
∵PE∥CF,
∴
=
,即
=
,
解得:a=
b,
∴a:b=
:1,
作GH⊥AC于H,
∵∠CAB=45°,
∴HG=
AG=
(2
b-2b)=(2-
)b,
又∵BG=2b-a=(2-
)b,
∴GH=GB,GH⊥AC,GB⊥BC,
∴∠HCG=∠BCG,
∵PE∥CF,
∴∠PEG=∠BCG,
∴∠AEC=∠ACB=45°.
∴AB=BC,BP=BF,
∴AP=CF,
在△APE和△CFE中,
∵
|
∴△APE≌△CFE,
∴EA=EC;
(2)△ACE是直角三角形,理由是:
如图2,∵P为AB的中点,
∴PA=PB,
∵PB=PE,
∴PA=PE,
∴∠PAE=45°,
又∵∠BAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
(3)设CE交AB于G,

∵EP平分∠AEC,EP⊥AG,
∴AP=PG=a-b,BG=a-(2a-2b)=2b-a,
∵PE∥CF,
∴
| PE |
| BC |
| PG |
| GB |
| b |
| a |
| a-b |
| 2b-a |
解得:a=
| 2 |
∴a:b=
| 2 |
作GH⊥AC于H,
∵∠CAB=45°,
∴HG=
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
又∵BG=2b-a=(2-
| 2 |
∴GH=GB,GH⊥AC,GB⊥BC,
∴∠HCG=∠BCG,
∵PE∥CF,
∴∠PEG=∠BCG,
∴∠AEC=∠ACB=45°.
看了 已知正方形ABCD,P为射线...的网友还看了以下:
过椭圆X的平方除以9加上Y的平方除以4等于1上任意一点P向圆X的平方加上Y的平方等于1引切线PA. 2020-04-12 …
过椭圆X的平方除以9加上Y的平方除以4等于1上任意一点P向圆X的平方加上Y的平方等于1引切线PA. 2020-04-12 …
描述:已知椭圆C的方程为x^2/4+y^2=1,A,B是四条直线x=±2,y=±1所围成的矩形的两 2020-07-12 …
在方格纸上有A,B两点,若以点B为原点建立直角坐标系,则点A的坐标为(3,4).若以A点为原点建立 2020-07-15 …
如图,在Rt△ABC中,∠B=90°,BC=53,∠C=30°.点D从点C出发沿CA方向以每秒2个 2020-07-17 …
初一数学题关于平面直角坐标在方格纸上有A,B两点,若以点B为原点建立平面直角坐标系,则点A的坐标为 2020-08-01 …
已知点A是圆F1:(x+3)2+y2=16上任意一点,点F2与点F1关于原点对称.线段AF2的中垂 2020-08-01 …
如图,在Rt△ABC中,∠B=90°,∠C=30°,AC=48,点D从点C出发沿CA方向以每秒4个 2020-08-03 …
平面直角坐标系若点P(x,y)在x轴上方,|x|=5,|y|=4,则P点的坐标为点P(x,y),若x 2020-11-01 …
后方交会至少需要几个已知点?后方交会定义:在待定点上向至少三个已知点进行水平角观测,并根据三个已知点 2020-11-07 …