如图，在平面直角坐标系中，已知点A在x正半轴，以点A为圆心作A，点M（4，4）在A上，直线y=-34x+b与圆相切于点M，分别交x轴、y轴于B、C两点．（1）直接写出b的值和点B的坐标；（2）求点A

Question

如图，在平面直角坐标系中，已知点A在x正半轴，以点A为圆心作 A，点M（4，4）在 A上，直线y=-(3)/(4)x+b与圆相切于点M，分别交x轴、y轴于B、C两点．

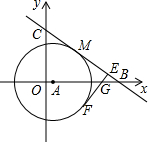
（1）直接写出b的值和点B的坐标；
（2）求点A的坐标和圆的半径；
（3）若EF切 A于点F分别交AB和BC于G、E，且FE⊥BC，求(GF)/(EG)的值．

Answer 1

（1）∵点M在直线y=-(3)/(4)x+b上，
∴-(3)/(4)×4+b=4，解得：b=7．
∴直线的解析式为y=-(3)/(4)x+7．
∵当y=0时，-(3)/(4)x+7=0，解得：x=(28)/(3)，
∴B（(28)/(3)，0）．
（2）∵BC是圆A的切线，
∴AM⊥BC．
设直线AM的解析式为y=(4)/(3)x+c．
∵将M（4，4）代入y=(4)/(3)x+c得(16)/(3)+c=4，解得：c=-(4)/(3)，
∴直线AM的解析式为y=(4)/(3)x-(4)/(3)．
∵当y=0时，(4)/(3)x-(4)/(3)=0，解得x=1，
∴A（1，0）．
∵由两点间的距离公式可知AM=√((4-1)2+(4-0)2)=5，
∴圆A的半径为5．
（3）如图1所示：连接AF、AM．

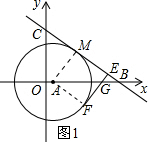
∵BC、EF是圆A的切线，
∴AM⊥BC，AF⊥EF．
又∵BC⊥EF，
∴∠AME=∠MEF=∠EFA=90°．
∴四边形AFEM为矩形．
又∵AM=AF，
∴四边形AFEM为正方形．
∴ME=AF=5．
∵在Rt△AMB中，MB=√(AB2-AM2)=(20)/(3)，
∴BE=BM-ME=(5)/(3)．
∵∠AFG=∠BEG=90°，∠AGF=∠BGE，
∴△AGF∽△BGE．
∴(FG)/(EG)=(AF)/(BE)即(GF)/(EG)=(5)/((5)/(3))．
∴(GF)/(EG)=3．