早教吧作业答案频道 -->数学-->
如图,四边形ABCD是O的内接四边形,延长DC,AB交于点E,且BE=BC.(1)求证:△ADE是等腰三角形;(2)若∠D=90°,O的半径为5,BC:DC=1:2,求△CBE的周长.
题目详情
如图,四边形ABCD是 O的内接四边形,延长DC,AB交于点E,且BE=BC.
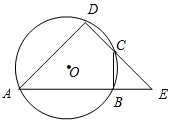
(1)求证:△ADE是等腰三角形;
(2)若∠D=90°, O的半径为5,BC:DC=1:
,求△CBE的周长.

(1)求证:△ADE是等腰三角形;
(2)若∠D=90°, O的半径为5,BC:DC=1:
| 2 |
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是 O的内接四边形,
∴∠A=∠BCE,
∵BE=BC,
∴∠BCE=∠BEC,
 ∴∠A=∠BEC,
∴∠A=∠BEC,
∴DA=DE,即△ADE是等腰三角形;
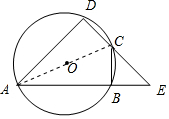
(2)连接AC,
设BC=k,则CD=
k,
∵∠D=90°,
∴∠CBE=∠D=90°,又BE=BC,
∴∠E=45°,
∴BE=BC=k,EC=
k,
∴DE=2
k,
由勾股定理得,AC=
k,
∵ O的半径为5,
∴
k=10,
解得,k=
,
∴△CBE的周长为:2
+2
.
∴∠A=∠BCE,
∵BE=BC,
∴∠BCE=∠BEC,
 ∴∠A=∠BEC,
∴∠A=∠BEC,∴DA=DE,即△ADE是等腰三角形;
(2)连接AC,
设BC=k,则CD=
| 2 |
∵∠D=90°,
∴∠CBE=∠D=90°,又BE=BC,
∴∠E=45°,
∴BE=BC=k,EC=
| 2 |
∴DE=2
| 2 |
由勾股定理得,AC=
| 10 |
∵ O的半径为5,
∴
| 10 |
解得,k=
| 10 |
∴△CBE的周长为:2
| 10 |
| 5 |
看了 如图,四边形ABCD是O的内...的网友还看了以下:
A,B,C是圆○上三点,∠BAC的平分线AM交BC于点D,交圆○于点M,若∠BAC等于60°,角A 2020-04-05 …
如图,在Rt△ABC中AC=BC,以A为圆心画弧DF,交AB于点D,交AC延长线于点F,交BC于E 2020-05-16 …
CP是等边△ABC外角∠ACE平分线,点D在射线BC上,以D为顶点、DA为一边作角ADF=60°, 2020-07-17 …
如图,平面直角坐标系中,A(1,0),B(0,1),C(-1,0),过点C的直线l绕点C旋转,交y 2020-07-20 …
在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是BC边上一点,BN⊥AD交AD的延长线于 2020-08-01 …
已知抛物线y=ax的二次方-bx+c与y轴交与点A(0,3),与x轴分别交与B(1,0),C(5, 2020-08-02 …
已知抛物线(y等于ax的平方减bx加c.).与y轴交于点A(0,3),与X轴分别交于B(1,0); 2020-08-02 …
已知抛物线y=ax²-bx+c与y轴交于点A(0,3),与x轴分别交于点B(1,0)、C(5,0) 2020-08-02 …
如图,在平面直角坐标系中,矩形OABC的边OC,OA分别与X,Y轴重合对角线BO等于六倍根号五,AB 2020-11-07 …
如图,在三角形abc中,ab=ac,以ab为直径的圆O交BC于点D,交AC于点E,过点D作DF垂直A 2020-12-25 …