已知椭圆C1：+=1（a1＞b1＞0）与双曲线C2：﹣=1（a2＞0，b2＞0）有相同的焦点F1，F2，点P是两曲线的一个公共点，a1，a2又分别是两曲线的离心率，若PF1⊥PF2，则4e12+e22的最小值为（）A．

Question

已知椭圆C₁： +=1（a₁＞b₁＞0）与双曲线C₂：﹣=1（a₂＞0，b₂＞0）有相同的焦点F₁，F₂，点P是两曲线的一个公共点，a₁，a₂又分别是两曲线的离心率，若PF₁⊥PF₂，则4e₁²+e₂²的最小值为（　　）

A．    B．4    C．    D．9

　

Answer 1

C【考点】双曲线的简单性质；椭圆的简单性质．

【专题】圆锥曲线中的最值与范围问题．

【分析】由题意设焦距为2c，椭圆长轴长为2a₁，双曲线实轴为2a₂，令P在双曲线的右支上，由已知条件结合双曲线和椭圆的定义推志出，由此能求出4e₁²+e₂²的最小值．

【解答】由题意设焦距为2c，椭圆长轴长为2a₁，双曲线实轴为2a₂，

令P在双曲线的右支上，

由双曲线的定义|PF₁|﹣|PF₂|=2a₂，①

由椭圆定义|PF₁|+|PF₂|=2a₁，②

又∵PF₁⊥PF₂，

∴=4c²，③

①²+②²，得=，④

将④代入③，得，

∴4e₁²+==+

=

≥=．

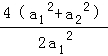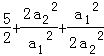
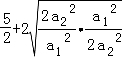故选：C．

【点评】本题考查4e₁²+e₂²的最小值的求法，是中档题，解题时要熟练掌握双曲线、椭圆的定义，注意均值定理的合理运用．