过双曲线x2-y215=1的右支上一点P，分别向圆C1：（x+4）2+y2=4和圆C2：（x-4）2+y2=4作切线，切点分别为M，N，则|PM|2-|PN|2的最小值为（）A.10B.13C.16D.19

Question

过双曲线x²-

(y2)/(15)=1的右支上一点P，分别向圆C₁：（x+4）²+y²=4和圆C₂：（x-4）²+y²=4作切线，切点分别为M，N，则|PM|²-|PN|²的最小值为（　　）

A. 10

B. 13

C. 16

D. 19

Answer 1

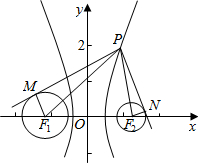圆C₁：（x+4）²+y²=4的圆心为（-4，0），半径为r₁=2；
圆C₂：（x-4）²+y²=1的圆心为（4，0），半径为r₂=1，
设双曲线x²-(y2)/(15)=1的左右焦点为F₁（-4，0），F₂（4，0），
连接PF₁，PF₂，F₁M，F₂N，可得
|PM|²-|PN|²=（|PF₁|²-r₁²）-（|PF₂|²-r₂²）
=（|PF₁|²-4）-（|PF₂|²-1）
=|PF₁|²-|PF₂|²-3=（|PF₁|-|PF₂|）（|PF₁|+|PF₂|）-3
=2a（|PF₁|+|PF₂|-3=2（|PF₁|+|PF₂|）-3≥2•2c-3=2•8-3=13．
当且仅当P为右顶点时，取得等号，
即最小值13．
故选：B．