早教吧作业答案频道 -->数学-->
如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.(1)求证:△ACE≌△BCD;(2)求证:BF⊥AE;(3)请判断∠CFE与∠CAB的大小关系并说明理由.
题目详情
如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.
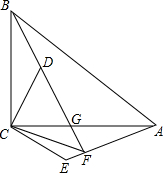
(1)求证:△ACE≌△BCD;
(2)求证:BF⊥AE;
(3)请判断∠CFE与∠CAB的大小关系并说明理由.

(1)求证:△ACE≌△BCD;
(2)求证:BF⊥AE;
(3)请判断∠CFE与∠CAB的大小关系并说明理由.
▼优质解答
答案和解析
证明:(1)∵BC⊥CA,DC⊥CE,
∴∠ACB=∠DCE=90°,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
,
∴△BCD≌△ACE;
(2)∵△BCD≌△ACE,
∴∠CBD=∠CAE,
∵∠BGC=∠AGE,
∴∠AFB=∠ACB=90°,
∴BF⊥AE;
(3)∠CFE=∠CAB,
过C作CH⊥AE于H,CI⊥BF于I,
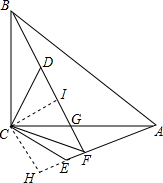 ∵△BCD≌△ACE,
∵△BCD≌△ACE,
∴AE=BD,S△ACE=S△BCD,
∴CH=CI,
∴CF平分∠BFH,
∵BF⊥AE,
∴∠BFH=90°,∠CFE=45°,
∵BC⊥CA,BC=CA,
∴△ABC是等腰直角三角形,
∴∠CAB=45°,
∴∠CFE=∠CAB.
∴∠ACB=∠DCE=90°,
∴∠BCD=∠ACE,
在△BCD与△ACE中,
|
∴△BCD≌△ACE;
(2)∵△BCD≌△ACE,
∴∠CBD=∠CAE,
∵∠BGC=∠AGE,
∴∠AFB=∠ACB=90°,
∴BF⊥AE;
(3)∠CFE=∠CAB,
过C作CH⊥AE于H,CI⊥BF于I,
 ∵△BCD≌△ACE,
∵△BCD≌△ACE,∴AE=BD,S△ACE=S△BCD,
∴CH=CI,
∴CF平分∠BFH,
∵BF⊥AE,
∴∠BFH=90°,∠CFE=45°,
∵BC⊥CA,BC=CA,
∴△ABC是等腰直角三角形,
∴∠CAB=45°,
∴∠CFE=∠CAB.
看了 如图,BC⊥CA,BC=CA...的网友还看了以下:
设f(x)=1/x,若f(x)+f(y)=f(z).求z..请问,这个答案中直接就写出了,f(y)= 2020-03-30 …
已知△BCE、△DCF分别是以平行四边形ABCD的邻边BC、CD为边向外所作的等边三角形求证:△A 2020-05-17 …
一道关于函数周期的题若函数f(x)在R上为奇函数,且在(-1,0)上为增函数,且f(x+2)=-f 2020-06-07 …
利用秦九韶算法求当x=2时,f(x)=1+2x+3x2+…+6x5的值,下列说法正确的是()A.先 2020-07-14 …
如图,P是菱形ABC尸对角线BD上一点,连接CP并延长,交AD于E,交BA延长线于F.(1)求证如 2020-07-16 …
已知正方形ABCD中,点E在BC上,连接AE,过点B作BF⊥AE于点G,交CD于点F.(1)如图1 2020-07-19 …
如图,在△ABC中,分别以AB,AC为边向外作△ABD和△ACE,且AD=AB,AE=AC,∠BA 2020-07-27 …
下面从集合P到集合Q的对应f为映射的是A.P={0,3,4},Q={-2,-√3,0,√3,2}, 2020-07-30 …
f(t)二阶可导x=t*f'(t)-f(t)y=f'(t)求y对x的二阶导数f(t)二阶可导即一阶 2020-08-02 …
如图,在△ABC中,AB=AC,E是AB的中点.以点E为圆心,EB为半径画弧,交BC于点D,连接ED 2020-11-23 …