早教吧作业答案频道 -->数学-->
如图,在△ABC中,分别以AB,AC为边向外作△ABD和△ACE,且AD=AB,AE=AC,∠BAD=∠CAE,连接DC,BE,点G,F分别是DC,BE的中点,连接AF,FG.(1)求证:DC=BE;(2)当∠BAD=80°时,连接AG,求∠AFG
题目详情
如图,在△ABC中,分别以AB,AC为边向外作△ABD和△ACE,且AD=AB,AE=AC,∠BAD=∠CAE,连接DC,BE,点G,F分别是DC,BE的中点,连接AF,FG.
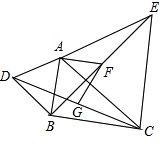
(1)求证:DC=BE;
(2)当∠BAD=80°时,连接AG,求∠AFG的度数;
(3)若∠BAD=α,请你直接写出∠AFG与α之间满足的数量关系.

(1)求证:DC=BE;
(2)当∠BAD=80°时,连接AG,求∠AFG的度数;
(3)若∠BAD=α,请你直接写出∠AFG与α之间满足的数量关系.
▼优质解答
答案和解析
(1)∵∠DAB=∠CAE,
∴∠DAB+∠BAC=∠CAE+∠BAC,
∴∠DAC=∠BAE.
在△ADC和△ABE中,
,
∴△ADC≌△ABE(SAS),
∴DC=BE;
(2)如图,连接AG.
∵△ADC≌△ABE,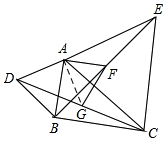
∴∠ADC=∠ABE,AD=AB.
∵G、F分别是DC与BE的中点,
∴DG=
DC,BF=
BE,
∴DG=BF.
在△ADG和△ABF中,
,
∴△ADG≌△ABF(SAS),
∴AG=AF,∠DAG=∠BAF,
∴∠AGF=∠AFG,∠DAG-∠BAG=∠BAF-∠BAG,
∴∠DAB=∠GAF.
∵∠DAB=80°,
∴∠GAF=80°.
∵∠GAF+∠AFG+∠AGF=180°,
∴∠AFG=
(180°-80°)=50°;
(3)∠AFG与α之间满足的数量关系为:∠AFG=90°-
α.
由(2)可得,当∠DAB=α时,∠GAF=α.
∵∠GAF+∠AFG+∠AGF=180°,
∴α+2∠AFG=180°,
∴∠AFG=90°-
α.
∴∠DAB+∠BAC=∠CAE+∠BAC,
∴∠DAC=∠BAE.
在△ADC和△ABE中,
|
∴△ADC≌△ABE(SAS),
∴DC=BE;
(2)如图,连接AG.
∵△ADC≌△ABE,

∴∠ADC=∠ABE,AD=AB.
∵G、F分别是DC与BE的中点,
∴DG=
| 1 |
| 2 |
| 1 |
| 2 |
∴DG=BF.
在△ADG和△ABF中,
|
∴△ADG≌△ABF(SAS),
∴AG=AF,∠DAG=∠BAF,
∴∠AGF=∠AFG,∠DAG-∠BAG=∠BAF-∠BAG,
∴∠DAB=∠GAF.
∵∠DAB=80°,
∴∠GAF=80°.
∵∠GAF+∠AFG+∠AGF=180°,
∴∠AFG=
| 1 |
| 2 |
(3)∠AFG与α之间满足的数量关系为:∠AFG=90°-
| 1 |
| 2 |
由(2)可得,当∠DAB=α时,∠GAF=α.
∵∠GAF+∠AFG+∠AGF=180°,
∴α+2∠AFG=180°,
∴∠AFG=90°-
| 1 |
| 2 |
看了 如图,在△ABC中,分别以A...的网友还看了以下:
如图是放在水平地面上的一把椅子的侧面图,椅子高为AC,椅面宽为BE,椅脚高为ED,且AC⊥BE,A 2020-05-15 …
如图,等腰直角三角形mbc中,角mbc=90,a、d分别为mb、m c的中点,连ac、bd,e为d 2020-05-24 …
已知:如图,在△ABC中,AD,BE分别是BC,AC边上的高,AD,BE相交于点F.求证:△AEF 2020-06-02 …
如图,BC=AC,AC垂直BC,AE垂直BE,D是BE和AC的交点,BD=2AE,BE=平分角AB 2020-06-15 …
如图,C为线段BD上一点(不与点B,D重合),在BD同侧分别作正三角形ABC和正三角形CDE,AD 2020-06-20 …
如图在三角形纸片ABC中角c=90度,AC=6,折叠该纸片使点c落在AB边上的点d处如图,在三角纸 2020-06-29 …
三角形abc的内角abc和外角ac的角平分线交于点e,be交ac于f,过点e做eg平行于bd交a三 2020-07-31 …
如图1,△ABC中,AB=AC,过B点作射线BE,过C点作射线CF,使∠ABE=∠ACF,且射线BE 2020-11-03 …
在平面直角坐标系中,点A在X轴的正半轴上点B在Y轴的正半轴上,BE平分∠ABF,AC平分∠OAB直线 2020-12-23 …
已知:△ABC是等边三角形,分别过点A,B作AF∥BC,BE∥AC,AF,BE分别与过点C的直线交于 2021-01-24 …