早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠ACB=90°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且AF=CE.(1)求证:点E是AB的中点;(2)求证:四边形ACEF是平行四边形.
题目详情
如图,在Rt△ABC中,∠ACB=90°,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且AF=CE.
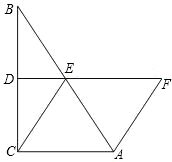
(1)求证:点E是AB的中点;
(2)求证:四边形ACEF是平行四边形.

(1)求证:点E是AB的中点;
(2)求证:四边形ACEF是平行四边形.
▼优质解答
答案和解析
(1)证明:∵∠ACB=90°,DE是BC的中垂线,
∴DE⊥BC,
又∵AC⊥BC,
∴DE∥AC,
又∵D为BC中点,DF∥AC,
∴DE是△ABC的中位线,
∴E为AB边的中点;
(2)证明:∵E为AB边的中点,
∴CE=AE=BE,
∵AF=CE,
∴CE=AE=AF,
∴∠ECA=∠EAC,∠AEF=∠F,
∵DE∥AC,
∴∠EAC=∠AEF,∠FEC+∠ECA=180°,
∴∠ECA=∠F,
∴∠FEC+∠F=180°,
∴AF∥CE,
∴四边形ACEF是平行四边形.
∴DE⊥BC,
又∵AC⊥BC,
∴DE∥AC,
又∵D为BC中点,DF∥AC,
∴DE是△ABC的中位线,
∴E为AB边的中点;
(2)证明:∵E为AB边的中点,
∴CE=AE=BE,
∵AF=CE,
∴CE=AE=AF,
∴∠ECA=∠EAC,∠AEF=∠F,
∵DE∥AC,
∴∠EAC=∠AEF,∠FEC+∠ECA=180°,
∴∠ECA=∠F,
∴∠FEC+∠F=180°,
∴AF∥CE,
∴四边形ACEF是平行四边形.
看了 如图,在Rt△ABC中,∠A...的网友还看了以下:
如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2 2020-05-23 …
如图,△ABC中,延长CB到D,使BD=BC,当E点在线段AD上移动时,若AE=λAB+μAC,则 2020-06-20 …
在长方体ABCD-A1B1C1D1中,AD=1,AA1=1=AB=2点E是AB上的动点,点M为D1 2020-07-09 …
如图所示,A、B两点分别是斜面的顶端、底端,C、D是斜面上的两个点,LAC:LCD:LDB=1:3 2020-07-29 …
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点 2020-07-30 …
(2009•邯郸二模)两个等腰直角三角形ABC,ADE,如图①摆放(E点在AB上),连BD,取BD 2020-08-03 …
初中的一道几何证明题等腰梯形,左上角A点,右上角B点,左下角C点,左下角D点,底边CD点上有一点E, 2020-10-31 …
如图①,在△ABC中,AD是三角形的高,且AD=6cm,E是一个动点,由B向C移动,其速度与时间的变 2020-11-03 …
如图,AB∥CD,AB=CD,点E、F在直线BC上,且E点在B点的右侧,F点在C点的右侧,BE=CF 2020-11-03 …
如图所示,△ABC是等腰三角形,E点在底边AB上,由A点向B点移动(不包括A、B两点),D、F分别在 2020-12-25 …