早教吧作业答案频道 -->数学-->
锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是()A、60°B、72°C、66°D、不确定
题目详情
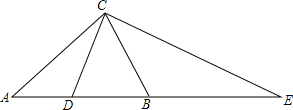 锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )
锐角△ABC中,AC=AB,CD是中线,延长AB到E使BE=AB,连接CE,此时△ACE为钝角三角形且∠DCB=36°,则∠DCE的度数是( )| A、60° | B、72° |
| C、66° | D、不确定 |
▼优质解答
答案和解析
考点:
等腰三角形的性质
专题:
分析:
取AC的中点F,连接BF,根据等腰三角形的轴对称性可得∠DCB=∠FBC,再判断出BF是△ACE的中位线,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得BF∥CE,根据两直线平行,内错角相等可得∠BCE=∠FBC,然后根据∠DCE=∠BCE+∠DCB计算即可得解.
如图,取AC的中点F,连接BF,∵AC=AB,CD是中线,∴∠DCB=∠FBC=36°,∵BE=AB,∴BF是△ACE的中位线,∴BF∥CE,∴∠BCE=∠FBC=36°,∴∠DCE=∠BCE+∠DCB=36°+36°=72°.故选B.
点评:
本题考查了等腰三角形的性质,三角形的中位线平行于第三边并且等于第三边的一半,难点在于作辅助线构造出三角形的中位线.
考点:
等腰三角形的性质
专题:
分析:
取AC的中点F,连接BF,根据等腰三角形的轴对称性可得∠DCB=∠FBC,再判断出BF是△ACE的中位线,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得BF∥CE,根据两直线平行,内错角相等可得∠BCE=∠FBC,然后根据∠DCE=∠BCE+∠DCB计算即可得解.
如图,取AC的中点F,连接BF,∵AC=AB,CD是中线,∴∠DCB=∠FBC=36°,∵BE=AB,∴BF是△ACE的中位线,∴BF∥CE,∴∠BCE=∠FBC=36°,∴∠DCE=∠BCE+∠DCB=36°+36°=72°.故选B.
点评:
本题考查了等腰三角形的性质,三角形的中位线平行于第三边并且等于第三边的一半,难点在于作辅助线构造出三角形的中位线.
看了 锐角△ABC中,AC=AB,...的网友还看了以下:
求角A+角B+角C+角D+角E+角F+角G的度数半个小时之内传上来, 2020-04-05 …
(1)第一张图片是一个五角形ABCDE,你能计算出角A+角B+角C+角D+角E(2)从左往右数第二 2020-04-26 …
帮我看看1.已知:如图,AB=AC,角ABD=角ACE,BD与CE相交于O点.求证:OB=OC2. 2020-04-26 …
如图 ,求角a+角b+角c+角d+角e+角f的度数如图所示,求角A+角B+角C+角D+角E+角F的 2020-05-15 …
平面上六点A,B,C,D,E,F构成如图所示的图形,则角A +角B+ 角C+角D+角E+角F 为多 2020-05-16 …
把一副三角尺按如图所示拼在一起,试确定图中角A,角B,叫AEB,角ACD的度数,并用大于左边是B 2020-05-16 …
设A=(101;020;-101)求满足方程AB+E=A^2+B的矩阵B用AB+E=A^2+B(A 2020-06-18 …
如果,在三角形ABC中,E是AB上的一点,D是BC延长线上的一点,DE交AC于点F(1)如果角D大 2020-06-23 …
如图直角梯形ABCD中AD平行BC,角A=角B=90°,AD=AB=4,BC=6.E是AB上一动点 2020-07-19 …
在三角形ABC中,角A角B的平分线分别交对边于D,E角C的外角平分线交对边延长线于F,求证:D、E 2020-08-03 …