早教吧作业答案频道 -->数学-->
如图1,在△ABC中,∠B=60°,点M从点B出发沿射线BC方向,在射线BC上运动.在点M运动的过程中,连结AM,并以AM为边在射线BC上方,作等边△AMN,连结CN.(1)当∠BAM=°时,AB=2BM;(2)
题目详情
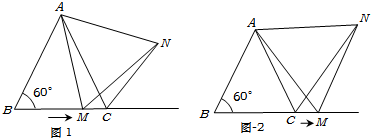
如图1,在△ABC中,∠B=60°,点M从点B出发沿射线BC方向,在射线BC上运动.在点M运动的过程中,连结AM,并以AM为边在射线BC上方,作等边△AMN,连结CN.
(1)当∠BAM=___°时,AB=2BM;
(2)请添加一个条件:___,使得△ABC为等边三角形;
①如图1,当△ABC为等边三角形时,求证:BM=CN;
②如图2,当点M运动到线段BC之外时,其它条件不变,①中结论BM=CN还成立吗?请说明理由.
(1)当∠BAM=___°时,AB=2BM;
(2)请添加一个条件:___,使得△ABC为等边三角形;
①如图1,当△ABC为等边三角形时,求证:BM=CN;
②如图2,当点M运动到线段BC之外时,其它条件不变,①中结论BM=CN还成立吗?请说明理由.

▼优质解答
答案和解析
(1)当∠BAM=30°时,
∴∠AMB=180°-60°-30°=90°,
∴AB=2BM;
故答案为:30;
(2)添加一个条件AB=AC,可得△ABC为等边三角形;
故答案为:AB=AC;
①∵△ABC与△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC-∠MAC=∠MAN-∠MAC,
即∠BAM=∠CAN,
在△BAM与△CAN中,
,
∴△BAM≌△CAN(SAS),
∴BM=CN;
②成立,理由如下;
∵△ABC与△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC+∠MAC=∠MAN+∠MAC,
即∠BAM=∠CAN,
在△BAM与△CAN中,
,
∴△BAM≌△CAN(SAS),
∴BM=CN.
∴∠AMB=180°-60°-30°=90°,
∴AB=2BM;
故答案为:30;
(2)添加一个条件AB=AC,可得△ABC为等边三角形;
故答案为:AB=AC;
①∵△ABC与△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC-∠MAC=∠MAN-∠MAC,
即∠BAM=∠CAN,
在△BAM与△CAN中,
|
∴△BAM≌△CAN(SAS),
∴BM=CN;
②成立,理由如下;
∵△ABC与△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC+∠MAC=∠MAN+∠MAC,
即∠BAM=∠CAN,
在△BAM与△CAN中,
|
∴△BAM≌△CAN(SAS),
∴BM=CN.
看了 如图1,在△ABC中,∠B=...的网友还看了以下:
Rt△ABC在平面直角坐标系中的初始位置如图1所示,∠C=90°,AB=6,AC=3.点A在x轴上 2020-05-16 …
在平面直角坐标系中,我们把横,纵坐标都是整数的点叫做整点.已知点{04},点B是X轴正半轴上的整点 2020-06-11 …
如图,已知过点a(1,0)的抛物线y=1/4x^2-1/4(b+1)x+b/4(b是实数)与x轴交 2020-06-14 …
如图,在数轴上有一条可以移动的线段AB.若将线段AB向右移动,使得点A移动到点B处,这时点B对应的 2020-07-16 …
已知数轴上点a和点b之间的距离为28个单位长度,点a在原点的左边,距离原点八个单位长度.点b在原点 2020-07-30 …
复数z在复平面内对应的点为A,将点A绕坐标原点,按逆时针方向旋转π2,再向左平移一个单位,向下平移 2020-08-01 …
复数z在复平面内对应的点为A,将点A绕坐标原点,按逆时针方向旋转π2,再向左平移一个单位,向下平移 2020-08-01 …
复数z在复平面内对应的点为A,将点A绕坐标原点,按逆时针方向旋转,再向左平移一个单位,向下平移一个 2020-08-01 …
x轴上的点坐标为0,y轴上的点坐标为0当B=时,点b(3,丨b-1丨)在第一、三象限角平分线上当B 2020-08-03 …
点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴 2020-11-04 …