早教吧作业答案频道 -->数学-->
如图,在等边△ABC中,P是BC下方一动点,且∠BPC=120°,PB、PC是关于x的方程(a-1)x2-9(a-1)x+b=c的两实数根,求PA的长.
题目详情
如图,在等边△ABC中,P是BC下方一动点,且∠BPC=120°,PB、PC是关于x的方程(a-1)x2-9(a-1)x+b=c的两实数根,求PA的长.


▼优质解答
答案和解析
延长BP到D,使得DP=PC,连接CD.
∵∠BPC=120,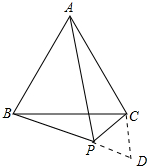
∴∠CPD=60.
又∵PC=PD,
∴△PCD是等边三角形,
∴PC=CD,∠PCD=60°,
∴∠ACB+∠BCP=PCD+∠BCP,
即∠ACP=∠BCD.
∵等边三角形ABC中,
∴BC=AC.
在△DBC和△PAC中,
,
∴△DBC≌△PAC,
∴AP=BD.
∵BD=BP+DP,
∴AP=BP+DP,
∵DP=PC,
∴PA=PB+PC.
∵PB、PC是关于x的方程(a-1)x2-9(a-1)x+b=c的两实数根,
∴PB+PC=9,
∴PA=9.
∵∠BPC=120,

∴∠CPD=60.
又∵PC=PD,
∴△PCD是等边三角形,
∴PC=CD,∠PCD=60°,
∴∠ACB+∠BCP=PCD+∠BCP,
即∠ACP=∠BCD.
∵等边三角形ABC中,
∴BC=AC.
在△DBC和△PAC中,
|
∴△DBC≌△PAC,
∴AP=BD.
∵BD=BP+DP,
∴AP=BP+DP,
∵DP=PC,
∴PA=PB+PC.
∵PB、PC是关于x的方程(a-1)x2-9(a-1)x+b=c的两实数根,
∴PB+PC=9,
∴PA=9.
看了 如图,在等边△ABC中,P是...的网友还看了以下:
知道题是这样的已知等差数列an的工差d不等于零前n项和为sn若s三等于a二的平方,且s一s二s四成 2020-05-13 …
冬天一个人A坐在雪橇上,假设他与雪橇的总重力为400N,B在他们的前方且角度向上30度拉他们,用3 2020-05-13 …
若X乘X的m次方乘X的n次方于于X的14方,且m比n大3,则m乘n的值为 2020-05-14 …
如果A=2x的5次方-3x的平方乘y的3次方+2y的5次方,B=2x的平方+xy-3y的平方,C= 2020-05-14 …
已知关于x的一次函数y=(3a-7)x+a-2的图像与y轴交点在x轴的上方,且y随x的增大而减小, 2020-05-16 …
一道求轨迹方程的数学题在三角形ABC中,已知A(-1,0)B(1,0)点C在AB的上方,且角ACB 2020-05-19 …
一道数学题,数论,指数函数a为正数,x=9a,且a的x方=x的a方,即a^x=x^a求a的值,最好 2020-06-03 …
2x的平方+5xy-7y的平方且y不等于0求x/y 2020-06-04 …
设矩阵A=(101030101),矩阵B=(KE+A)的平方,且K属于R.1)求对角阵D,使B与D 2020-06-06 …
若a+4根号3=(m+n根号3)的平方,且a、m、n均为正整数,求a的值 2020-06-24 …