早教吧作业答案频道 -->数学-->
某研究性学习小组进行了探究活动,在△ABC中,∠C=90°,AB=10,AC=6,点O是AB的中点,将一块直角三角板的直角顶点绕点O旋转,图中的M、N分别为直角三角形的直角边与AC、BC的交点.(1)
题目详情
某研究性学习小组进行了探究活动,在△ABC中,∠C=90°,AB=10,AC=6,点O是AB的中点,将一块直角三角板的直角顶点绕点O旋转,图中的M、N分别为直角三角形的直角边与AC、BC的交点.
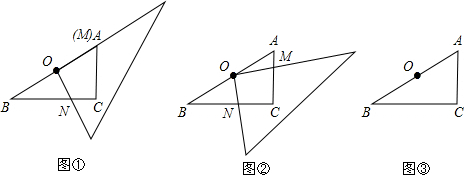
(1)如图①,当三角板的一条直角边与OB重合时,点M与点A也重合,
①求此时CN的长;②写出AC2、CN2、BN2满足的数量关系___;
(2)当三角板旋转到如图②所示的位置时,即点M在AC上(不与A、C重合),
①猜想图②中AM2、CM2、CN2、BN2这四条线段满足的数量关系:___;
②说明你得出此结论的理由.
(3)若在三角板旋转的过程中满足CM=CN,请你利用图③并联系上述结论,求出此时BN的长.

(1)如图①,当三角板的一条直角边与OB重合时,点M与点A也重合,
①求此时CN的长;②写出AC2、CN2、BN2满足的数量关系___;
(2)当三角板旋转到如图②所示的位置时,即点M在AC上(不与A、C重合),
①猜想图②中AM2、CM2、CN2、BN2这四条线段满足的数量关系:___;
②说明你得出此结论的理由.
(3)若在三角板旋转的过程中满足CM=CN,请你利用图③并联系上述结论,求出此时BN的长.
▼优质解答
答案和解析
(1)①∵∠C=90°,AB=10,AC=6,
∴BC=
=8,
∵点O是AB的中点,
∴BO=
AB=5,
∵∠BON=∠C=90°,
∵∠B=∠B,
∴△BNO∽△BAC,
∴
=
,
∴
=
,
∴BN=
,
∴CN=BC-BN=
;
②如图①,连接AN,
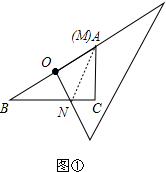 ∵NO⊥AB,AO=BO,
∵NO⊥AB,AO=BO,
∴AN=BN,
在Rt△ACN中,AN2=AC2+CN2,
即BN2=AC2+CN2,
故答案为:BN2=AC2+CN2;
(2)①AM2+BN2=NC2+MC2;
②如图2,延长MO,使OK=MO,连接KB,NM,NK,
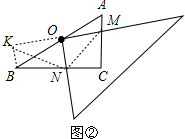 在△KOB和△MOA中,
在△KOB和△MOA中,
,
∴△KOB≌△MOA,
∴KB=AM,KO=MO,∠A=∠KBO,
∵NO⊥MO,
∴NK=NM,
∵∠A+∠ABC=90°,
∴∠MBO+∠ABC=90°,
在Rt△KBN,Rt△MNC中,KB2+BN2=KN2,NC2+MC2=NM2,
∴KB2+BN2=NC2+MC2,
即AM2+BN2=NC2+MC2;
故答案为:AM2+BN2=NC2+MC2;
(3)∵(2)①中已经证明:AM2+BN2=CN2+CM2,
设CM=CN=x,则BN=8-x,AM=6-x,
代入上式得:x=
,
∴BN=
.
∴BC=
| AB2-AC2 |
∵点O是AB的中点,
∴BO=
| 1 |
| 2 |
∵∠BON=∠C=90°,
∵∠B=∠B,
∴△BNO∽△BAC,
∴
| BO |
| BC |
| BN |
| AB |
∴
| 5 |
| 8 |
| BN |
| 10 |
∴BN=
| 25 |
| 4 |
∴CN=BC-BN=
| 7 |
| 4 |
②如图①,连接AN,
 ∵NO⊥AB,AO=BO,
∵NO⊥AB,AO=BO,∴AN=BN,
在Rt△ACN中,AN2=AC2+CN2,
即BN2=AC2+CN2,
故答案为:BN2=AC2+CN2;
(2)①AM2+BN2=NC2+MC2;
②如图2,延长MO,使OK=MO,连接KB,NM,NK,
 在△KOB和△MOA中,
在△KOB和△MOA中,
|
∴△KOB≌△MOA,
∴KB=AM,KO=MO,∠A=∠KBO,
∵NO⊥MO,
∴NK=NM,
∵∠A+∠ABC=90°,
∴∠MBO+∠ABC=90°,
在Rt△KBN,Rt△MNC中,KB2+BN2=KN2,NC2+MC2=NM2,
∴KB2+BN2=NC2+MC2,
即AM2+BN2=NC2+MC2;
故答案为:AM2+BN2=NC2+MC2;
(3)∵(2)①中已经证明:AM2+BN2=CN2+CM2,
设CM=CN=x,则BN=8-x,AM=6-x,
代入上式得:x=
| 25 |
| 7 |
∴BN=
| 31 |
| 7 |
看了 某研究性学习小组进行了探究活...的网友还看了以下:
试猜想:以a,b,c为边的三角形是直角三角形吗?请说明理由.(a=n²-1b=2nc=n²+1n>1 2020-03-30 …
在三角形ABC中,内角A.B.C对边的边长为a.b.c,已知c=2,C=pai/3.若三角形面积为 2020-04-05 …
在三角形ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C=60度.若三角形ABC 2020-04-05 …
三角形ABC的内角A,B,C所对的边分别为a,b,c,它的外接圆半径为6,三边a,b,c,角A,B 2020-05-16 …
圆o的半径为r,其内接正三角形,正方形,正六边形的边长为a,b,c(1)求a,b,c的值(2)以a 2020-06-03 …
已知:如图,△ABD和△ACE均为等边三角形,且∠DAB=∠CAE=60°,那么△ADC≌△AEB 2020-06-04 …
在三角形ABC中,如果AB边上的高与AB边的长相等,则AC/BC+BC/AC+AB^2/BC*AC 2020-07-22 …
求高手指教三角形四心到三边距离之比的证明!三角形内心到a,b,c三边距离之比=1:1:1;三角形外 2020-07-30 …
在三角形ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,C=π/3,(1)若三角形A 2021-02-07 …
已知三角形ABC的内角A,B,C所对的边分别为a,b,c,.已知三角形ABC的内角A,B,C所对的边 2021-02-07 …