早教吧作业答案频道 -->数学-->
已知抛物线y=ax2+bx+c(a<0)经过点A(-3,0)、B(1,0),且与y轴交于点C,设抛物线的顶点为D.(1)求点C、D的坐标(用含a的式子表示);(2)当a变化时,△ACD能否为直角三角形?若能
题目详情
已知抛物线y=ax2+bx+c(a<0)经过点A(-3,0)、B(1,0),且与y轴交于点C,设抛物线的顶点为D.
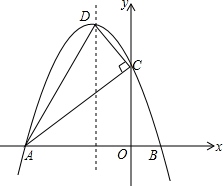
(1)求点C、D的坐标(用含a的式子表示);
(2)当a变化时,△ACD能否为直角三角形?若能?求出所有符合条件的a的值;若不能,请说明理由.

(1)求点C、D的坐标(用含a的式子表示);
(2)当a变化时,△ACD能否为直角三角形?若能?求出所有符合条件的a的值;若不能,请说明理由.
▼优质解答
答案和解析
(1)∵抛物线y=ax2+bx+c(a<0)经过点A(-3,0)、B(1,0),
∴可以假设抛物线为y=a(x+3)(x-1)=a(x2+2x-3)=a(x+1)2-4a,
∴顶点D(-1,-4a),
令x=0得y=-3a,得点C(0,-3a),
∴点C(0,-3a),点D(-1,-4a).
(2)①若∠ADC=90°则有AC2=AD2+DC2,
∴9+9a2=4+16a2+1+a2,
∴a2=
,
∵a<0,
∴a=-
.
②若∠DCA=90°则有AD2=AC2+CD2,
∴4+16a2=9+9a2+1+a2,
∴a2=1,
∵a<0,
∴a=-1,
综上所述a=-1或-
.
∴可以假设抛物线为y=a(x+3)(x-1)=a(x2+2x-3)=a(x+1)2-4a,
∴顶点D(-1,-4a),
令x=0得y=-3a,得点C(0,-3a),
∴点C(0,-3a),点D(-1,-4a).
(2)①若∠ADC=90°则有AC2=AD2+DC2,
∴9+9a2=4+16a2+1+a2,
∴a2=
| 1 |
| 2 |
∵a<0,
∴a=-
| ||
| 2 |
②若∠DCA=90°则有AD2=AC2+CD2,
∴4+16a2=9+9a2+1+a2,
∴a2=1,
∵a<0,
∴a=-1,
综上所述a=-1或-
| ||
| 2 |
看了 已知抛物线y=ax2+bx+...的网友还看了以下:
急.已知集合A={(x,y)│x的平方+mx-y+2=0} ,B={(x,y)│x-y+1=0 , 2020-05-16 …
初三数学 二次函数:如图所示,已知抛物线与x轴相交于A(m,0)如图所示,已知抛物线与x轴相交于A 2020-05-16 …
已知集合A={(X,Y)丨2X-Y=0}B={(X.Y)丨3X+Y=0}C={(X,Y)丨2X-Y 2020-06-23 …
某下岗职工购进一批香蕉,到集贸市场零售.已知卖出的香蕉数量x与销售额y的关系如表所示:数量x(千克 2020-06-28 …
1.实数xyz满足x+y+z-2(xy+yz+zx)+4xyz=0.5证明x.y.z中至少有一个恰 2020-07-09 …
如图所示,已知直线L经过A(4,0)和B(0,4)两点,它与抛物线y=a(x的平方)在第……(数学 2020-07-13 …
1.设平面内有四个向量a,b,x,y,满足a=y-x,b=2x-y,a⊥b,|a|=|b|=1(1 2020-07-30 …
用matlab,已知x的值,和f(x,y)=0的隐函数,如何求y已知x=linspace(-2.23 2020-11-01 …
1.已知inti=0,x=1,y=0;在下列选项使i的值变成1的语句是().(A)if(x&&y)i 2020-11-01 …
一个电子仪器由两个部件构成,以X和Y分别表示两个部件的寿命(单位:千小时),已知X和Y的联合分布函数 2020-12-07 …