早教吧作业答案频道 -->数学-->
如图,△ABC中,AD是BC边上的高,CE是AB边上的中线,且DC=AE,G是CE的中点,连结DG.(1)求证:DG⊥CE;(2)作∠BEC的角平分线交BC于F,求证:BE+BF=EC.
题目详情
如图,△ABC中,AD是BC边上的高,CE是AB边上的中线,且DC=AE,G是CE的中点,连结DG.
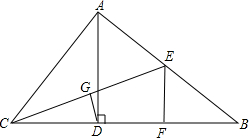
(1)求证:DG⊥CE;
(2)作∠BEC的角平分线交BC于F,求证:BE+BF=EC.

(1)求证:DG⊥CE;
(2)作∠BEC的角平分线交BC于F,求证:BE+BF=EC.
▼优质解答
答案和解析
证明:(1)连接DE,
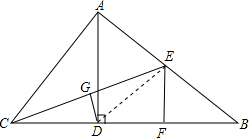
∵RT△ABD中,E是AB中点,
∴AE=DE,
∵CD=AE,
∴CD=DE,
∵G是CE中点,
∴DG⊥CE;
(2)延长CB到H使BH=BE,连接EH,
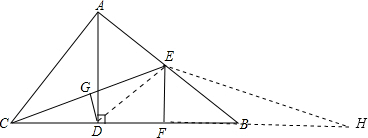
∵AD是BC边上的高,CE是AB边上的中线,
∴RT△ADB中AE=BE=DE,
∵DC=AE,
∴AE=BE=DE=DC,
∴∠BDE=∠DBE,
∵∠BDE+∠CDE=∠DBE+∠EBH=180°,
∴∠CDE=∠EBH,
在△CDE和△EBH中,
,
∴△CDE≌△EBH(SAS),
∴∠DCE=∠BEH,EC=EH,
∵∠EFH=∠DCE+∠CEF,∠FEH=∠BEH+∠BEF,
∵EF是∠BEC的角平分线,
∴∠CEF=∠BEF,
∴∠EFH=∠FEH,
∴EH=FH,
∵FH=BH+BF=BE+BF,
∴BE+BF=EC.

∵RT△ABD中,E是AB中点,
∴AE=DE,
∵CD=AE,
∴CD=DE,
∵G是CE中点,
∴DG⊥CE;
(2)延长CB到H使BH=BE,连接EH,

∵AD是BC边上的高,CE是AB边上的中线,
∴RT△ADB中AE=BE=DE,
∵DC=AE,
∴AE=BE=DE=DC,
∴∠BDE=∠DBE,
∵∠BDE+∠CDE=∠DBE+∠EBH=180°,
∴∠CDE=∠EBH,
在△CDE和△EBH中,
|
∴△CDE≌△EBH(SAS),
∴∠DCE=∠BEH,EC=EH,
∵∠EFH=∠DCE+∠CEF,∠FEH=∠BEH+∠BEF,
∵EF是∠BEC的角平分线,
∴∠CEF=∠BEF,
∴∠EFH=∠FEH,
∴EH=FH,
∵FH=BH+BF=BE+BF,
∴BE+BF=EC.
看了 如图,△ABC中,AD是BC...的网友还看了以下:
在矩形ABCD中,AB=5cm,BC=13cm,在DC边上一点E沿着AE把△AED折叠,使点D正好 2020-05-15 …
如图,四边形ABCD是平行四边形,AE⊥CB,交CB的延长线于点E,AF⊥CD,交CD的延长线于点 2020-05-16 …
已知点O为等边△ABD的边BD的中点,现将一个∠α=120゜的角放在点O处,∠α的两边分别交直线A 2020-06-12 …
C为线段AE上的一点,分别以AC.CE为边在AE的同侧做等边三角形ABC和等边三角形CDE,连接A 2020-06-27 …
` 如图,C为线段AE上的一点,分别以AC,CE为边在AE的同侧作等边 △ABC和等边△CDE,连 2020-06-27 …
C为线段AE上的一点,分别以AC,CE为边在AE的同侧作等边 △ABC和等边△CDE,连接AD,B 2020-06-27 …
正方形中证明题正方形ABCD中BC边中点E,边接AE.边E做EF垂直AE交正方形ABCD的外角平分 2020-07-13 …
已知四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,∠ABC=120°,∠MBN=60°,将 2020-07-18 …
已知等腰直角三角形AOB,∠AOB=90°,一直角三角板的直角顶点放在等腰三角形斜边中点C上,将此 2020-07-26 …
我虽然新手还没有什么积分,不过日后我一定会报答你的在平行四边形ABCD中,过点B作BE垂直CD,垂足 2020-12-31 …