早教吧作业答案频道 -->数学-->
如图,在菱形ABCD中,∠BAD=60°,M为对角线BD延长线上一点,连接AM和CM,E为CM上一点,且满足CB=CE,连接BE,交CD于点F.(1)若∠AMB=30°,且DM=3,求BE的长;(2)证明:AM=CF+DM.
题目详情
如图,在菱形ABCD中,∠BAD=60°,M为对角线BD延长线上一点,连接AM和CM,E为CM上一点,且满足CB=CE,连接BE,交CD于点F.
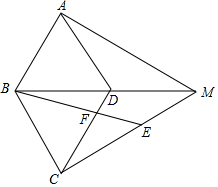
(1)若∠AMB=30°,且DM=3,求BE的长;
(2)证明:AM=CF+DM.

(1)若∠AMB=30°,且DM=3,求BE的长;
(2)证明:AM=CF+DM.
▼优质解答
答案和解析
(1) 如图1中,
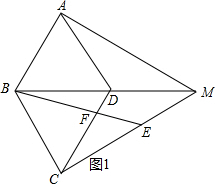
∵四边形ABCD是菱形,∠BAD=60°,
∴△ABD,△BCD的是等边三角形,
∴∠ABD=∠CBD=∠ADB=∠BAD=60°,BA=BC,
∵∠AMB=30°,∠ADB=∠AMB+∠DAM,
∴∠DAM=∠DMA=30°,
∴∠BAM=90°,DA=DM=AB=BC=CE=3,
在△BMA和△BMC中,
,
∴△BMA≌△BMC,
∴∠BCM=∠BAM=90°,
在Rt△BCE中,BE=
=3
.
(2)如图2中,在BD上取一点G,使得BG=DF,连接CG交BE于O.

∵BG=DF,∠CBG=∠BDF,BD=BC,
∴△GBC≌△FDB,
∴∠BGC=∠BFD,∠DBF=∠BCG,
∴∠MGC=∠BFC,
∵∠COF=∠CBO+∠OCB=∠CBO+∠DBF=60°
在△COE中,∠ECO+∠EOC+∠CEO=180°,
在△BCF中,∠BFC+∠CBF+∠BCF=180°,
∵CB=CE,
∴∠CBE=∠CEO,∵∠BCF=∠COE=60°,
∴∠ECO=∠BFC=∠MGC,
∴MC=MG,
由(1)可知△BMA≌△BMC,
∴AM=MC=MG,
∵MG=DG+DM,
∵BD=CD,BG=DF,
∴DG=CF,
∴AM=CF+DM

∵四边形ABCD是菱形,∠BAD=60°,
∴△ABD,△BCD的是等边三角形,
∴∠ABD=∠CBD=∠ADB=∠BAD=60°,BA=BC,
∵∠AMB=30°,∠ADB=∠AMB+∠DAM,
∴∠DAM=∠DMA=30°,
∴∠BAM=90°,DA=DM=AB=BC=CE=3,
在△BMA和△BMC中,
|
∴△BMA≌△BMC,
∴∠BCM=∠BAM=90°,
在Rt△BCE中,BE=
| BC2+CE2 |
| 2 |
(2)如图2中,在BD上取一点G,使得BG=DF,连接CG交BE于O.

∵BG=DF,∠CBG=∠BDF,BD=BC,
∴△GBC≌△FDB,
∴∠BGC=∠BFD,∠DBF=∠BCG,
∴∠MGC=∠BFC,
∵∠COF=∠CBO+∠OCB=∠CBO+∠DBF=60°
在△COE中,∠ECO+∠EOC+∠CEO=180°,
在△BCF中,∠BFC+∠CBF+∠BCF=180°,
∵CB=CE,
∴∠CBE=∠CEO,∵∠BCF=∠COE=60°,
∴∠ECO=∠BFC=∠MGC,
∴MC=MG,
由(1)可知△BMA≌△BMC,
∴AM=MC=MG,
∵MG=DG+DM,
∵BD=CD,BG=DF,
∴DG=CF,
∴AM=CF+DM
看了 如图,在菱形ABCD中,∠B...的网友还看了以下:
等腰三角形周长16CM,且一条腰是5CM,求其他两条边的长 等腰三角形周长16CM,且一条长是5C 2020-05-16 …
一个等腰三角形各边都是整数,且周长为20,那么满足条件且形状不同的等腰三角形共有种?还有:在△AB 2020-05-20 …
英语翻译洪钧陶万类大块禀群生明闇信异姿静躁亦殊形自予及有识志不在功名虚恬窃所好文学少所经忝荷既过任 2020-06-03 …
有一个长方形和一个正方形木块,且长方形棱长之和与正方形棱长之和都是144cm,长方形的长18cm, 2020-06-04 …
等边三角形菱形证明正三角形CEF的边长与菱形ABCD的边长相等(C是两图形的公共顶点,三角形再菱形 2020-06-08 …
已知三角形ABC的三边长abc且其中任意两边长均不相等1/a1/b1/c成等差数列,1比较更号b/ 2020-07-10 …
已知a、b、c为三角形三边长,且方程b(x2-1)-2ax+c(x2+1)=0有两个相等的实数根. 2020-08-02 …
点P是线段AB的黄金分割点,且AP>BP,设以AP为边长的正方形的面积为S1,以PB为宽、以AB为 2020-08-02 …
1.有一张长方形纸,长是96厘米,宽是60厘米,现在把这张长方形纸分成若干个相同的正方形,要使长方形 2020-11-03 …
小明的爷爷开了一个玻璃店,有一次他为小明做了一只带盖的长方体形状的玻璃缸(盖子是活动的且可密封).小 2020-11-03 …