早教吧作业答案频道 -->数学-->
如图,△ABC中,三个内角B、A、C成等差数列,且AC=10,BC=15(1)求△ABC的面积;(2)已知平面直角坐标系xOy,点D(10,0),若函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<π2)的图象绕过A
题目详情
如图,△ABC中,三个内角B、A、C成等差数列,且AC=10,BC=15
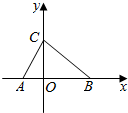
(1)求△ABC的面积;
(2)已知平面直角坐标系xOy,点D(10,0),若函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<
)的图象绕过A、C、D三点,且A、D为f(x)的图象与x轴相邻的两个交点,求f(x)的解析式.

(1)求△ABC的面积;
(2)已知平面直角坐标系xOy,点D(10,0),若函数f(x)=Msin(ωx+φ)(M>0,ω>0,|φ|<
| π |
| 2 |
▼优质解答
答案和解析
(1)在△ABC中,∵角B、A、C成等差数列,
∴2A=B+C,即3A=180°,则A=60° …(1分)
由余弦定理可知:a2=b2+c2-2bccos60°,…(2分)
∴c2-10c-125=0,
则c=|AB|=5+5
. …(4分)
又∵|AO|=10cos60°=5,
∴|BO|=5
,
则△ABC的面积S=
(5+5
)×5
=
(3
+
).…(6分)
(2)T=2×(10+5)=30,
∴ω=
. …(8分)
∵f(-5)=Msin[
×(-5)+φ]=0,
∴sin(-
+φ)=0,
则-
+φ=kπ,即φ=
+kπ,k∈Z
∵|φ|<
,∴φ=
,…(10分)
∵f(0)=Msin
=5
,
∴M=10,
则f(x)=10sin(
x+
).…(12分)
∴2A=B+C,即3A=180°,则A=60° …(1分)
由余弦定理可知:a2=b2+c2-2bccos60°,…(2分)
∴c2-10c-125=0,
则c=|AB|=5+5
| 6 |
又∵|AO|=10cos60°=5,
∴|BO|=5
| 6 |
则△ABC的面积S=
| 1 |
| 2 |
| 6 |
| 3 |
| 25 |
| 2 |
| 2 |
| 3 |
(2)T=2×(10+5)=30,
∴ω=
| π |
| 15 |
∵f(-5)=Msin[
| π |
| 15 |
∴sin(-
| π |
| 3 |
则-
| π |
| 3 |
| π |
| 3 |
∵|φ|<
| π |
| 2 |
| π |
| 3 |
∵f(0)=Msin
| π |
| 3 |
| 3 |
∴M=10,
则f(x)=10sin(
| π |
| 15 |
| π |
| 3 |
看了 如图,△ABC中,三个内角B...的网友还看了以下:
平面直角坐标系中四边形的存在性问题在平面直角坐标中,有点O(0,0),A(-1,1),B(2,2)( 2020-03-31 …
如图1,在平面直角坐标中,直角梯形OABC的顶点A的坐标为(4,0),直线y=-x+3经过顶点B, 2020-05-13 …
如图1,在平面直角坐标中,直角梯形OABC的顶点A的坐标为(4,0),直线y=-14x+3经过顶点 2020-06-12 …
154直角坐标如何转化为极坐标拜托各位了3Q直角坐标中x^2+y^2=2ax转化为极坐标后是怎样的 2020-06-27 …
在平面直角坐标中,抛物线y等于负x平方加2x加3,点A(负1,0)点P(2,3)和点Q都在抛物线上 2020-07-19 …
在平面直角坐标中xOy中,曲线C1的参数方程是x=1-2ty=2t(t是参数),曲线C2的普通方程 2020-07-31 …
在平面直角坐标中,以原点为极点,x轴正半轴为极轴建立极坐标第.设椭圆的长轴长为10,中心为(3,0 2020-07-31 …
如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=9 2020-08-01 …
在平面直角坐标中,三角形ABO的顶点A的坐标为(2,1),O为坐标原点,点B与A点关于Y轴对称,求三 2020-11-03 …
如图,△ABC在平面直角坐标中,边OB与x轴重合,∠AOB=∠OAB=30°,点B的坐标是(2,0) 2020-12-25 …