早教吧作业答案频道 -->数学-->
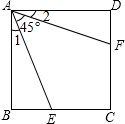
如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:①∠1=∠2=22.5°;②点C到EF的距离是2-1;③△ECF的周长为2;④BE+DF>EF.其中正确的结论是
题目详情
如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°;
②点C到EF的距离是
-1;
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是___.(写出所有正确结论的序号)
①∠1=∠2=22.5°;
②点C到EF的距离是
| | 2 |
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是___.(写出所有正确结论的序号)

▼优质解答
答案和解析
∵四边形ABCD为正方形,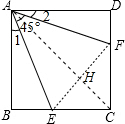
∴AB=AD,∠BAD=∠B=∠D=90°,
在Rt△ABE和Rt△ADF中
,
∴Rt△ABE≌Rt△ADF,
∴∠1=∠2,
∵∠EAF=45°,
∴∠1=∠2=∠22.5°,所以①正确;
连结EF、AC,它们相交于点H,如图,
∵Rt△ABE≌Rt△ADF,
∴BE=DF,
而BC=DC,
∴CE=CF,
而AE=AF,
∴AC垂直平分EF,AH平分∠EAF,
∴EB=EH,FD=FH,
∴BE+DF=EH+HF=EF,所以④错误;
∴△ECF的周长=CE+CF+EF=CED+BE+CF+DF=CB+CD=1+1=2,所以③正确;
设BE=x,则EF=2x,CE=1-x,
∵△CEF为等腰直角三角形,
∴EF=
CE,即2x=
(1-x),解得x=
-1,
∴EF=2(
-1),
∴CH=
EF=
-1,所以②正确.
故答案为①②③.

∴AB=AD,∠BAD=∠B=∠D=90°,
在Rt△ABE和Rt△ADF中
|
∴Rt△ABE≌Rt△ADF,
∴∠1=∠2,
∵∠EAF=45°,
∴∠1=∠2=∠22.5°,所以①正确;
连结EF、AC,它们相交于点H,如图,
∵Rt△ABE≌Rt△ADF,
∴BE=DF,
而BC=DC,
∴CE=CF,
而AE=AF,
∴AC垂直平分EF,AH平分∠EAF,
∴EB=EH,FD=FH,
∴BE+DF=EH+HF=EF,所以④错误;
∴△ECF的周长=CE+CF+EF=CED+BE+CF+DF=CB+CD=1+1=2,所以③正确;
设BE=x,则EF=2x,CE=1-x,
∵△CEF为等腰直角三角形,
∴EF=
| 2 |
| 2 |
| 2 |
∴EF=2(
| 2 |
∴CH=
| 1 |
| 2 |
| 2 |
故答案为①②③.
看了 如图,已知正方形ABCD边长...的网友还看了以下:
已知函数f(x)定义域为R,且对任意实数x,y满足f(x+y)=f(x)f(y),给出以下四个结论 2020-05-13 …
设有关系模式R(A,B,C,D,E,F) ,其函数依赖集为F={E→D,C→B,CE→F,B→A}。 2020-05-23 …
设有关系模式R(A,B,C,D,E,F),其函数依赖集为F={E→D,C→B,CE→F,B→A}。则 2020-05-24 …
A、B、C、D、E、F、G、H均为初中化学常见物质,其中C、D、F为单质,其余为化合物,A是赤铁矿 2020-06-09 …
ab设(0,+∞)上的连续函数f使得积分值∫f(x)dx与a无关,其中a,b>0,求证:f(x)= 2020-06-12 …
一个9位数abcdefghi满足:1.a+b+...+h+i=cd2.a(b+d-c)=243.( 2020-07-19 …
给出一棵树的逻辑结构T=(K,R),其中K={A,B,C,D,E,F,G,H,I,J}R={r}r 2020-07-22 …
)已知函数f(x)=log2x-2log2(x+c),其中c>0.若已知函数f(x)=log2x- 2020-07-23 …
sql自定义求和函数与计算列的用法做一个分数统计表,列a,b,c,d,e,f,其sql自定义求和函数 2020-11-08 …
一个9位数abcdefghi满足:1.a+b+...+h+i=cd2.a(b+d-c)=243.(e 2020-11-19 …