早教吧作业答案频道 -->数学-->
如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.因为∠1=∠2=80°(已知),所以AB∥CD()所以∠BGF+∠3=180°()因为∠2+∠EFD=180°(邻补角的意义
题目详情
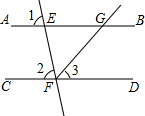
如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.
因为∠1=∠2=80°(已知),
所以AB∥CD(___)
所以∠BGF+∠3=180°(___)
因为∠2+∠EFD=180°(邻补角的意义).
所以∠EFD=___.(等式性质).
因为FG平分∠EFD(已知).
所以∠3=___∠EFD(角平分线的意义).
所以∠3=___.(等式性质).
所以∠BGF=___.(等式性质).
因为∠1=∠2=80°(已知),
所以AB∥CD(___)
所以∠BGF+∠3=180°(___)
因为∠2+∠EFD=180°(邻补角的意义).
所以∠EFD=___.(等式性质).
因为FG平分∠EFD(已知).
所以∠3=___∠EFD(角平分线的意义).
所以∠3=___.(等式性质).
所以∠BGF=___.(等式性质).

▼优质解答
答案和解析
因为∠1=∠2=80°(已知),
所以AB∥CD(同位角相等,两直线平行),
所以∠BGF+∠3=180°(两直线平行,同旁内角互补).
因为∠2+∠EFD=180°(邻补角的意义).
所以∠EFD=100°.(等式性质).
因为FG平分∠EFD(已知).
所以∠3=
∠EFD(角平分线的意义).
所以∠3=50°.(等式性质).
所以∠BGF=130°.(等式性质).
故答案为:同位角相等,两直线平行;两直线平行,同旁内角互补;100°;
;50°;130°.
所以AB∥CD(同位角相等,两直线平行),
所以∠BGF+∠3=180°(两直线平行,同旁内角互补).
因为∠2+∠EFD=180°(邻补角的意义).
所以∠EFD=100°.(等式性质).
因为FG平分∠EFD(已知).
所以∠3=
| 1 |
| 2 |
所以∠3=50°.(等式性质).
所以∠BGF=130°.(等式性质).
故答案为:同位角相等,两直线平行;两直线平行,同旁内角互补;100°;
| 1 |
| 2 |
看了 如图,已知直线AB、CD被直...的网友还看了以下:
我们把离心率为e=(√5+1)/2的双曲线x^2/a^2-y^2/b^2=1(a>0,b>0)成为我 2020-03-30 …
问几道二次根式的题(急~)1.1/(1+根号2-根号3)+2/(2+根号3-根号6)+3/(3-根 2020-05-13 …
已知abc是三角形abc的三边长,且满足a^2*c^2-b^2*c^2=a^4-b^4判断三角形a 2020-06-08 …
20.x^2/a^2+y^2/b^2+z^2/c^2=1成立;20.x^2/a^2+y^2/b^2 2020-06-11 …
利用(a+b+c)^2=a^2+b^2^c^2+2ab+2ac+abc,推导(a+b+c)^2+a 2020-07-30 …
圆锥曲线问题已知与曲线C:x^2+y^2-2x-2y+1=0相切的直线L交x轴、y轴于A、B两点, 2020-08-02 …
在△ABC中,已知a2+b2-c2=1/2bc,(1)求sin2(A+B)/2+cos2B的值;( 2020-08-02 …
1.-mx^n-1y^m+1(mn为常数)的系数和次数的和是.2.当m=何值时,(m+2)x^m^2 2020-10-31 …
已知双曲线x^2/a^2-y^2/b^2=1(a,b>0)的两条渐进线均和圆C:已知双曲线x^2/a 2020-11-01 …
在△ABC中,a^2+c^2-b^2=ac,log4SinA+log4SinC=-1,且三角形面积为 2021-02-07 …