早教吧作业答案频道 -->数学-->
如图所示的一块长方体木料中,已知AB=BC=4,AA1=1,设E为底面ABCD的中心,且AF=λAD(0≤λ≤12),则
题目详情
如图所示的一块长方体木料中,已知AB=BC=4,AA1=1,设E为底面ABCD的中心,且
=λ
(0≤λ≤
),则该长方体中经过点A1、E、F的截面面积的最小值为___.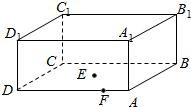
| |
| AF |
| |
| AD |
| 1 |
| 2 |

▼优质解答
答案和解析
设截面为A1FMN,显然A1FMN为平行四边形,过A点作AG⊥MF与G,则MG⊥A1G,作MK⊥AD与K,
根据题意AF=4λ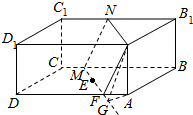 ,则CM=DK=4λ,KF=4-8λ,MF=
,则CM=DK=4λ,KF=4-8λ,MF=
,
易知Rt△MKF∽Rt△AGF,∴
=
,∴AG=
,
∴A1G2=AG2+AA12=
+1,
∴S截面2=MF2×A1G2=MF2×(
+1)=162λ2+42+(4-8λ)2
=32(10λ2-2λ+1)=320(λ-
)2+
(0≤λ≤
),
∴当λ=
时,S截面2=取得最小值
,此时S截面为
.
故答案为:
.
根据题意AF=4λ
 ,则CM=DK=4λ,KF=4-8λ,MF=
,则CM=DK=4λ,KF=4-8λ,MF=| 42+(4-8λ)2 |
易知Rt△MKF∽Rt△AGF,∴
| KM |
| MF |
| AG |
| 4λ |
| 16λ |
| MF |
∴A1G2=AG2+AA12=
| (16λ)2 |
| MF2 |
∴S截面2=MF2×A1G2=MF2×(
| (16λ)2 |
| MF2 |
=32(10λ2-2λ+1)=320(λ-
| 1 |
| 10 |
| 144 |
| 5 |
| 1 |
| 2 |
∴当λ=
| 1 |
| 10 |
| 144 |
| 5 |
12
| ||
| 5 |
故答案为:
12
| ||
| 5 |
看了 如图所示的一块长方体木料中,...的网友还看了以下:
在长方体ABCD-A1B1C1D1中,E,P分别是BC,A1D1的中点,M,N分别是AE,CD1的 2020-05-16 …
空间向量问题在平行六面体ABCD-A1B1C1D1中,设向量AA1=a(向量),向量AB=b,向量 2020-05-16 …
在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,点P为对角线AC1上的动点,点Q 2020-05-17 …
已知直三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,AB⊥BC,且AB=BC=AA1=2, 2020-05-17 …
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AB=2,BC=1 2020-06-26 …
如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,AA1=3.(1 2020-06-27 …
如图1,AA1∥BA2,过B1作AA1的平行线中,则∠A1,∠A1B1A2,∠A2之间的数量关系为 2020-07-09 …
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90° 2020-07-09 …
如图,直三棱柱ABC-A1B1C1中,已知AC=BC=AA1=a,∠ACB=90°,D是A1B1中 2020-07-17 …
在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角 2020-07-19 …