早教吧作业答案频道 -->数学-->
如图,正方体AC1中,已知O为AC与BD的交点,M为DD1的中点.(1)求异面直线B1O与AM所成角的大小.(2)求二面角B1-MA-C的正切值.
题目详情
如图,正方体AC1中,已知O为AC与BD的交点,M为DD1的中点.
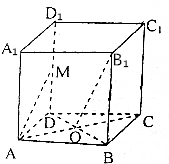
(1)求异面直线B1O与AM所成角的大小.
(2)求二面角B1-MA-C的正切值.

(1)求异面直线B1O与AM所成角的大小.
(2)求二面角B1-MA-C的正切值.
▼优质解答
答案和解析
 (1)∵BB1⊥平面ABCD,OB⊥AC,
(1)∵BB1⊥平面ABCD,OB⊥AC,
∴B1O⊥AC.设棱长为2
连接MO、MB1,则MO=
,B1O=
,MB1=3.
∵MO2+B1O2=MB12,∴∠MOB1=90°.
∴B1O⊥MO.
∵MO∩AC=O,∴B1O⊥平面MAC.
∴B1O⊥AM,
∴异面直线B1O与AM所成角为90°;
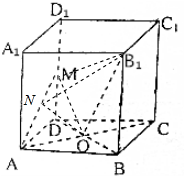
(2)作ON⊥AM于点N,连接B1N.
∵B1O⊥平面MAC,∴AM⊥平面B1ON.
∴B1N⊥AM.
∴∠B1NO就是二面角B1-MA-C的平面角.
∵AM=
,CM=
,∴AM=CM.
又O为AC的中点,∴OM⊥AC.则ON=OAsin∠MAO=
.
在Rt△B1ON中,tan∠B1NO=
=
,
∴∠B1NO=arctan
,即所求二面角的大小为arctan
.
 (1)∵BB1⊥平面ABCD,OB⊥AC,
(1)∵BB1⊥平面ABCD,OB⊥AC,∴B1O⊥AC.设棱长为2
连接MO、MB1,则MO=
| 3 |
| 6 |
∵MO2+B1O2=MB12,∴∠MOB1=90°.
∴B1O⊥MO.
∵MO∩AC=O,∴B1O⊥平面MAC.
∴B1O⊥AM,
∴异面直线B1O与AM所成角为90°;
(2)作ON⊥AM于点N,连接B1N.
∵B1O⊥平面MAC,∴AM⊥平面B1ON.
∴B1N⊥AM.
∴∠B1NO就是二面角B1-MA-C的平面角.
∵AM=
| 5 |
| 5 |
又O为AC的中点,∴OM⊥AC.则ON=OAsin∠MAO=
| ||
|
在Rt△B1ON中,tan∠B1NO=
| B1O |
| ON |
| 5 |
∴∠B1NO=arctan
| 5 |
| 5 |
看了 如图,正方体AC1中,已知O...的网友还看了以下:
1、设随机变量ξ满足P(ξ=1)=P,P(ξ=0)=1-P,求Eξ和Dξ2、设随机变量ξ满足P(ξ 2020-05-15 …
已知数列{an}(n≥0)满足a0=0,a1=1,对于所有正整数n,有an+1=2an+2007a 2020-05-17 …
一次函数求坐标题在补充里谢谢已知直线y=2x+1(1)求已知直线与y轴的交点坐标(2)若直线y=k 2020-05-21 …
将抛物线y=a(x+2)^2(a大于0)向右平移2个单位后与直线AB交与BC两点已知A(2,0)B 2020-06-19 …
已知直线l经过点P(2,3)且被两条平行直线3x+4y-7=0和3x+4y+8=0截得的线段长为d 2020-06-27 …
MOD算法:已知(17d)mod396=1,求d?答案是233,求具体计算过程! 2020-07-19 …
已知等差数列an的首项为1,公差为d,前n项和为An等比数列bn的首项为1,公比为q前n项和为Bn 2020-07-30 …
因式分解25x^2-4y^2(x+y)^2-6z(x+y)+9Z^2若a(x^my^4)/(3x^2 2020-10-31 …
已知BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD对角线AC,BD交于E.(1)求已知 2020-11-03 …
己知关于x的方程X2-2(k一1)X+K2=0有两个实数根X1,X2(1)试求k的取值范围(2)若| 2021-01-12 …