早教吧作业答案频道 -->数学-->
(1)证法回顾证明:三角形中位线定理.已知:如图1,DE是△ABC的中位线.求证:.证明:添加辅助线:如图1,在△ABC中,延长DE(D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF
题目详情
(1)【证法回顾】证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.
求证:___.
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;请继续完成证明过程:
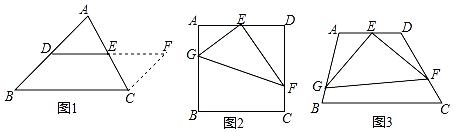
(2)【问题解决】如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)【拓展研究】如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=3
,DF=2,∠GEF=90°,求GF的长.
已知:如图1,DE是△ABC的中位线.
求证:___.
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;请继续完成证明过程:

(2)【问题解决】如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)【拓展研究】如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=3
| | 2 |
▼优质解答
答案和解析
(1)DE∥BC,DE=
BC,
证明: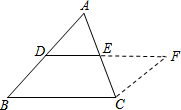 如图,延长DE 到点F,使得EF=DE,连接CF
如图,延长DE 到点F,使得EF=DE,连接CF
在△ADE和△CFE中,
,
∴△ADE≌△CFE(SAS),
∴∠A=∠ECF,AD=CF,
∴CF∥AB,
又∵AD=BD,
∴CF=BD,
∴四边形BCFD是平行四边形,
∴DE∥BC,DE=
BC.
故答案为:DE∥BC,DE=
BC.
(2)如图2,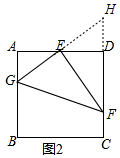 延长GE、FD交于点H,
延长GE、FD交于点H,
∵E为AD中点,
∴EA=ED,且∠A=∠EDH=90°,
在△AEG和△DEH中,
∴△AEG≌△DEH(ASA),
∴AG=HD=2,EG=EH,
∵∠GEF=90°,
∴EF垂直平分GH,
∴GF=HF=DH+DF=2+3=5;
(3)如图3,过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,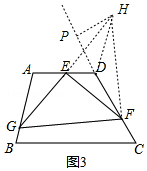
同(1)可知△AEG≌△DEH,GF=HF,
∴∠A=∠HDE=105°,AG=HD=3
,
∵∠ADC=120°,
∴∠HDF=360°-105°-120°=135°,
∴∠HDP=45°,
∴△PDH为等腰直角三角形,
∴PD=PH=3,
∴PF=PD+DF=3+2=5,
在Rt△HFP中,∠HPF=90°,HP=3,PF=5,
∴HF=
═
∴GF=
.
| 1 |
| 2 |
证明:
 如图,延长DE 到点F,使得EF=DE,连接CF
如图,延长DE 到点F,使得EF=DE,连接CF在△ADE和△CFE中,
|
∴△ADE≌△CFE(SAS),
∴∠A=∠ECF,AD=CF,
∴CF∥AB,
又∵AD=BD,
∴CF=BD,
∴四边形BCFD是平行四边形,
∴DE∥BC,DE=
| 1 |
| 2 |
故答案为:DE∥BC,DE=
| 1 |
| 2 |
(2)如图2,
 延长GE、FD交于点H,
延长GE、FD交于点H,∵E为AD中点,
∴EA=ED,且∠A=∠EDH=90°,
在△AEG和△DEH中,
|
∴△AEG≌△DEH(ASA),
∴AG=HD=2,EG=EH,
∵∠GEF=90°,
∴EF垂直平分GH,
∴GF=HF=DH+DF=2+3=5;
(3)如图3,过点D作AB的平行线交GE的延长线于点H,过H作CD的垂线,垂足为P,连接HF,

同(1)可知△AEG≌△DEH,GF=HF,
∴∠A=∠HDE=105°,AG=HD=3
| 2 |
∵∠ADC=120°,
∴∠HDF=360°-105°-120°=135°,
∴∠HDP=45°,
∴△PDH为等腰直角三角形,
∴PD=PH=3,
∴PF=PD+DF=3+2=5,
在Rt△HFP中,∠HPF=90°,HP=3,PF=5,
∴HF=
| HP2+FP2 |
| 34 |
∴GF=
| 34 |
看了 (1)证法回顾证明:三角形中...的网友还看了以下:
如图,在梯形ABCD中,AD//BC,E是CD的中点,连接AE并延长交BC的延长线于点F.若AB= 2020-05-16 …
在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.⑴求证:AB=CF; 2020-05-16 …
(2013•防城港模拟)如图所示,理想变压器的原线圈接到交流电源上,副线圈接有灯泡L,电路中分别接 2020-07-19 …
一理想变压器的原,副线圈的匝数比为3:1,在原、副线圈的回路中分别接有阻值相同的电阻,原线圈一侧接 2020-07-21 …
物理老师在实验室做“流体压强与流速关系”的演示实验:图甲所示的是由粗细不同的三节塑料管A、B、C连 2020-07-21 …
如图1已知在圆O中,点C为劣弧AB的中点,连接AC并延长至D,使CD=CA,连接DB并延长交圆O如 2020-07-31 …
如图所示,为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上, 2020-08-01 …
(2010•天津)为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流 2020-08-01 …
如图所示,一理想变压器的原、副线圈的匝数比为2:1,在原、副线圈的回路中分别接有阻值相同的电阻R,原 2020-12-27 …
一理想变压器的原、副线圈的匝数比为2:1,在原、副线圈的回路中分别接有阻值相同的电阻,原线圈一侧接在 2020-12-27 …