早教吧作业答案频道 -->数学-->
如图,抛物线y=-12x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).(1)求抛物线的表达式;(2)在抛物线的对称轴上是否存在点P,使△PCD
题目详情
如图,抛物线y=-
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由.
| 1 |
| 2 |

(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由.
▼优质解答
答案和解析
(1)∵抛物线y=-
x2+mx+n经过A(-1,0),C(0,2).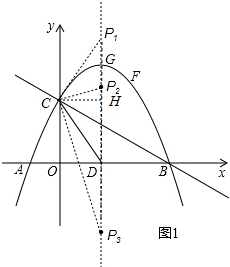
解得:
,
∴抛物线的解析式为:y=-
x2+
x+2;
(2)∵y=-
x2+
x+2,
∴y=-
(x-
)2+
,
∴抛物线的对称轴是直线x=
.
∴OD=
.
∵C(0,2),
∴OC=2.
在Rt△OCD中,由勾股定理,得
CD=
.
∵△CDP是以CD为腰的等腰三角形,
∴CP1=DP2=DP3.
作CH⊥x轴于H,
∴HP1=HD=2,
∴DP1=4.
∴P1(
,4),P2(
,
),P3(
,-
).
| 1 |
| 2 |

解得:
|
∴抛物线的解析式为:y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)∵y=-
| 1 |
| 2 |
| 3 |
| 2 |
∴y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
∴抛物线的对称轴是直线x=
| 3 |
| 2 |
∴OD=
| 3 |
| 2 |
∵C(0,2),
∴OC=2.
在Rt△OCD中,由勾股定理,得
CD=
| 5 |
| 2 |
∵△CDP是以CD为腰的等腰三角形,
∴CP1=DP2=DP3.
作CH⊥x轴于H,
∴HP1=HD=2,
∴DP1=4.
∴P1(
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
看了 如图,抛物线y=-12x2+...的网友还看了以下:
如果在数轴上表示a和b两个数的点的位置,那么化简|a-b|+|a+b|的结果是多少?a在0的左边, 2020-04-27 …
f(x)在[0 2a]上连续,f(0)=f(2a) 证明f(x)=f(x+a)在 (0 a)内至少 2020-05-13 …
下列情形时,如果a>0,抛物线y=ax²+bx+c的顶点在什么位置?1,方程ax²+bx+c=0有 2020-05-16 …
下列情形时,如果a>0,抛物线y=ax2bxc的顶点在什么位置? 2020-06-04 …
下列情形时,如果a>0,抛物线y=ax2+bx+c的顶点在什么位置? 2020-06-04 …
地理如何分东西我都要疯了……譬如说画一个数轴,中间是0度经线,左右是180度经线,这样,如果A在0 2020-07-01 …
如图,抛物线y=ax2+4经过x轴上的一点A(-2,0),抛物线顶点为点C,P是抛物线上的一动 2020-07-26 …
下列情形时,如果a>0,抛物线y=ax2+bx+c的顶点在什么位置? 2020-07-30 …
一道关于函数的题.关于函数y=(1/x)sin(1/x)的说法正确的是:A在(0,1]上有界B当x 2020-07-31 …
有理数a、b、c在数轴上的位置如图所示,试简化|a+b|-|b-2|-|a-c|-|2-c|图发不上 2020-11-20 …